Exercise 5.5Z: About the Rake Receiver

Two-way channel
& rake receiver

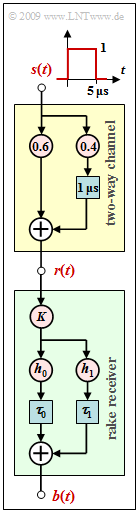
The diagram shows a two-way channel (yellow background). The corresponding descriptive equation is:

$$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$

Let the delay on the secondary path be $τ = 1 \ \rm µ s$.

Drawn below is the structure of a rake receiver (green background) with general coefficients $K$, $h_0$, $h_1$, $τ_0$ and $τ_1$.

The purpose of the rake receiver is to combine the energy of the two signal paths, making the decision more reliable.

The combined impulse response of the channel (German: "Kanal" ⇒ subscript "K") and the rake receiver can be expressed in the form

$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$

but only if the rake coefficients $h_0$, $h_1$, $τ_0$ and $τ_1$ are appropriately chosen.

The main part of $h_{\rm KR}(t)$ is supposed to be at $t = τ$.
The constant $K$ is to be chosen so that the amplitude of the main path $A_1 = 1$ :

$$K= \frac{1}{h_0^2 + h_1^2}.$$

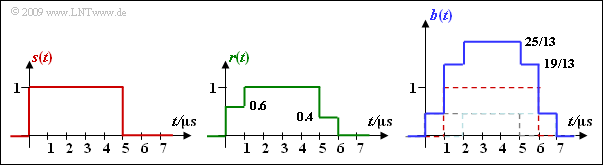
Apart from the rake parameters, the signals $r(t)$ and $b(t)$ are sought when $s(t)$ is a rectangle of height $s_0 = 1$ and width $T = \ \rm 5 µ s$.

Notes:

The exercise belongs to the chapter Error Probability of Direct-Sequence Spread Spectrum Modulation.
Reference is made in particular to the section Principle of the rake receiver.

Questions

Solution

(1) Solution 1 is correct:

The impulse response $h_{\rm K}(t)$ is obtained as the received signal $r(t)$ when there is a Dirac delta pulse at the input ⇒ $s(t) = δ(t)$. It follows that:

$$ h_{\rm K}(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$

(2) Solutions 2 and 3 are correct:

By definition, the channel frequency response $H_{\rm K}(f)$ is the Fourier transform of the impulse response $h_{\rm K}(t)$. With the shift theorem this results in:

$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$

Accordingly, the first proposed solution is incorrect in contrast to the other two:

$H_{\rm K}(f)$ is complex-valued and
the magnitude is periodic with $1/τ$, as the following calculation shows:

$$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau).$$

For $f = 0$, $|H_{\rm K}(f)| = 1$. This value is repeated in the respective frequency spacing $1/τ$.

(3) We first set $K = 1$ as agreed.

Altogether we get from $s(t)$ to the output signal $b(t)$ via four paths.
To satisfy the given $h_{\rm KR}(t)$ equation, either $τ_0 = 0$ must hold or $τ_1 = 0$. With $τ_0 = 0$ we obtain for the impulse response:

$$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$

To be able to focus the "main energy" at a certain time point, $τ_1 = τ$ would have to be chosen.
With $h_0 = 0.6$ and $h_1 = 0.4$, we then obtain $A_0 ≠ A_2$:

$$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) +0.48 \cdot \delta (t - \tau) + 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$

In contrast, with $h_0 = 0.6$, $h_1 = 0.4$, $τ_0 = τ$ and $τ_1 = 0$:

$$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t - \tau ) + 0.4 \cdot h_0 \cdot \delta (t - 2\tau) + 0.6 \cdot h_1 \cdot \delta (t) + 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.24 \cdot \delta (t ) +0.52 \cdot \delta (t - \tau) + 0.24 \cdot \delta (t - 2\tau) \hspace{0.05cm}.$$

Here, the additional condition $A_0 = A_2$ is satisfied. Thus, the result we are looking for is:

$$ \underline{\tau_0 = \tau = 1\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm}\tau_1 =0} \hspace{0.05cm}.$$

(4) The following must apply to the normalization factor:

$$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52} \hspace{0.15cm}\underline {\approx 1.923} \hspace{0.05cm}.$$

This gives for the common impulse response $($it holds $0.24/0.52 = 6/13)$:

$$ h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$

Signals to illustrate the rake receiver

(5) Statements 1 and 4 are correct, as shown in the diagram:

For the received signal $r(t)$ holds:

$$r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm µ s})\hspace{0.05cm},$$

and for the rake output signal $b(t)$:

$$b(t) = \frac{6}{13} \cdot s(t) + 1 \cdot s (t - 1\,{\rm µ s}) + \frac{6}{13} \cdot s (t - 2\,{\rm µ s}) \hspace{0.05cm}.$$

The overshoot of the output signal ⇒ $b(t) > 1$ is due to the normalization factor $K = 25/13$.
With $K = 1$, the maximum value of $b(t)$ would actually be $1$.

	The maximum value of $r(t)$ is $1$.
	The width of $r(t)$ is $7 \ µ s$.
	The maximum value of $b(t)$ is $1$.
	The width of $b(t)$ is $7 \ µ s$.

	$h_{\rm K}(t)$ consists of two Dirac delta functions.
	$h_{\rm K}(t)$ is complex-valued.
	$h_{\rm K}(t)$ is a function periodic with delay time $\tau$.

	$H_{\rm K}(f = 0) = 2$ is true.
	$H_{\rm K}(f)$ is complex-valued.
	$\|H_{\rm K}(f)\|$ is a function periodic with frequency $1/τ$.