Exercise 5.6: OFDM Spectrum
In this Exercise, we consider an OFDM system with $N = 4$ carriers.
- For simplicity, we restrict ourselves to a single time interval $T$.
- The frame duration is also $T_{\rm R} = T.$
- Accordingly, a guard interval is not used.
With the summary of pulse shaping and modulation by the function
- $$ g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm otherwise} \\ \end{array} \right.$$
the (complex) OFDM transmitted signal in the considered time interval $(0 ≤ t < T)$ results to:
- $$ s (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu} \cdot g_\mu (t )}.$$
All carrier coefficients $a_0$, $a_1$, $a_2$ and $a_3$ are either $0$ or $\pm 1$.
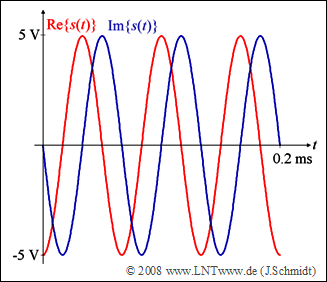
The diagram shows the real and imaginary parts of the transmitted signal $s(t)$ for a given combination of $a_0$, ... , $a_3$,
which is to be determined in subtask (3).
Notes:
- The exercise belongs to the chapter General Description of OFDM.
- Reference is made in particular to the pages
- OFDM - System consideration in the time domain,
- OFDM - System consideration in the frequency domain with causal basic pulse.
Questions
Solution
- The amplitude $s_0 \hspace{0.15cm}\underline { = 5\ \rm V}$ can be taken directly from the diagram.
(2) Furthermore, the symbol duration $T\hspace{0.15cm}\underline { = 0.2\ \rm ms}$ can be seen from the diagram.
- From this the basic frequency results to $f_0 = 1/T = 5\ \rm kHz$.
(3) In the example shown, there is only one frequency, namely $3 · f_0$.
- From this follows $a_0 = a_1 = a_2 \hspace{0.15cm}\underline { = 0}$ and for the range $0 ≤ t < T$:
- $$s(t) = a_3 \cdot s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2 \pi}} \hspace{0.04cm}\cdot \hspace{0.04cm} 3 f_0 \hspace{0.04cm}\cdot \hspace{0.04cm} t}= a_3 \cdot s_0 \cdot \cos ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \rm{j} \cdot a_3 \cdot s_0 \cdot \sin ({\rm{2 \pi}} \cdot 3 f_0 \cdot t).$$
- Comparison with the sketch $($real part: minus cosine, imaginary part: minus sine$)$ gives the following result:
- $$a_3\hspace{0.15cm}\underline {= -1}.$$
(4) The second solution is correct:
- The magnitude function is: $ |s(t)| = a_3 \cdot s_0 \cdot \sqrt{\cos^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \sin^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t)}= a_3 \cdot s_0.$
- However, this equation is valid only in the range of symbol duration $T$.
- This means: The OFDM principle works only with a time limit on $T$.
(5) In general, for the OFDM spectrum:
- $$S (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu } \cdot \,} {\rm{sinc}}(T \cdot (f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi}} \hspace{0.04cm}\cdot \hspace{0.04cm}{T}/{2}\hspace{0.04cm}\cdot \hspace{0.04cm} (f - \mu \cdot f_0 )} .$$
- The $\rm sinc$ function results from the time limit on $T$, and the last term in the sum results from the displacement law.
- By the zero crossings of the $\rm sinc$ function at the distance $f_0$ as well as $\rm sinc(0) = 1$ one obtains
- $$S(f = μ · f_0) = s_0 · T · a_μ.$$
- With $s_0 = 5 \ \rm V$ and $T = 0.2 \ \rm ms$ ⇒ $s_0 · T = 1\ \rm mV/Hz$ it further holds:
- $$ \mu = 0,\hspace{0.1cm} a_0 = 0\text{:}\hspace{0.95cm} S (f = 0) \hspace{0.15cm}\underline {= 0},\hspace{8cm}.$$
- $$\mu = 1, \hspace{0.1cm}a_1 = +1\text{:}\hspace{0.55cm} S (f = 5\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}},$$
- $$ \mu = 2, \hspace{0.1cm}a_2 = -1\text{:}\hspace{0.55cm} S (f = 10\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= -1\,\,{\rm{mV/Hz}}},$$
- $$ \mu = 3, \hspace{0.1cm}a_3 = +1\text{:}\hspace{0.55cm} S (f = 15\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= +1\,\,{\rm{mV/Hz}}}.$$
(6) Both statements are correct:
- The orthogonality with respect to the frequency domain has already been shown in subtask (5).
- The orthogonality with respect to the time domain results from the limitation of the individual symbols to the time duration $T$.