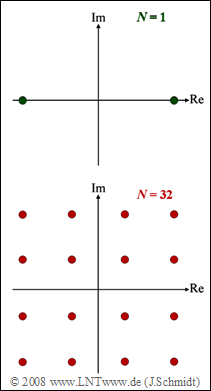
Exercise 5.6Z: Single-Carrier and Multi-Carrier System
From LNTwww
(Redirected from Exercise 5.6Z: Single and Multiple Beam System)
In this exercise, a comparison is to be made between
- a single-carrier $\rm (SC)$ system $(N = 1)$, and
- a multi-carrier $\rm (MC)$ system with $N = 32$ carriers.
For both transmission systems (see diagram), a data bit rate of $R_{\rm B} = 1 \ \rm Mbit/s$ is required in each case.
Notes:
- The exercise belongs to the chapter General Description of OFDM.
- Reference is also made to the chapter Quadrature Amplitude Modulation.
Questions
Solution
(1) From the diagram on the front page, it is immediately apparent that the single-carrier system is based on "binary phase modulation" $\rm (BPSK)$ ⇒ solution 2.
(2) In contrast, the multi-carrier system is based on $\rm 16–QAM$ ⇒ solution 4.
(3) In general, for an OFDM system with $N$ carriers and $M$ signal space points, the symbol duration is:
- $$T = N \cdot {\rm{log}_2}\hspace{0.04cm}(M) \cdot T_{\rm{B}}.$$
- Because of $R_{\rm{B}} = 1 \ \rm Mbit/s$, the bit duration for BPSK is equal to $T_{\rm{B}} = 1 \ \rm µ s$.
- From this, the symbol duration of the single-carrier system with $N = 1$ and $M = 2$ is:
- $$ T_{\rm{SC}} = 1 \cdot {\rm{log}_2}\hspace{0.04cm}(2) \cdot T_{\rm{B}}\hspace{0.15cm}\underline {= 1\,\,{\rm µ s}}.$$
(4) Similarly, for the multi-carrier system with $N = 32$ and $M = 16$, we obtain:
- $$T_{\rm{MC}} = 32 \cdot {\rm{log}_2}\hspace{0.04cm}(16) \cdot T_{\rm{B}}\hspace{0.15cm}\underline {= 128\,\,{\rm µ s}}.$$
(5) Solution 2 is correct because:
- At large symbol duration, the relative fraction extending from the predecessor symbol into the symbol under consideration and thus causing intersymbol interference $\rm (ISI)$ is smaller than at small symbol duration.