Exercise 5.8: Matched Filter for Colored Interference
At the input of a filter there is a Gaussian pulse
- $$g(t) = g_0 \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t} \right)^2 }$$
with amplitude $g_0 = 2 \hspace{0.08cm}\rm V$ and equivalent pulse duration $\Delta t = 1 \hspace{0.08cm}\rm ms$.
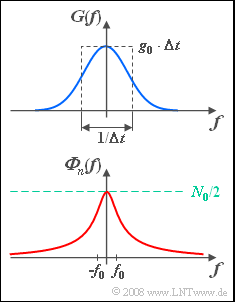
- The corresponding spectral function $G(f)$ is sketched above.
- The energy of this Gaussian pulse is given as follows:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2(t) \ {\rm{d}}t = \frac{g_0 ^2 \cdot \Delta t}{\sqrt 2 }} = 2.83 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}} {\rm{s}}.$$
An interference $n(t)$ is superimposed on the impulse $g(t)$, which largely covers the impulse.
Two alternatives are considered for this purpose:
- Let the bilateral interference power density be constant (only for the first subtask):
- $${\it \Phi}_n (f) = \frac{N_0 }{2},\quad N_0 = 10^{ - 6} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$
- Let the interference signal $n(t)$ be colored with the following interference power-spectral density $\rm (PSD)$:
- $${\it \Phi}_n (f) = \frac{N_0 /2}{{1 + \left( {f/f_0 } \right)^2 }},\quad f_0 = 500\;{\rm{Hz}}.$$
This second PSD response can be modeled, for example, from white noise by a shape filter with frequency response (first order low-pass):
- $$H_{\rm N}(f) = \frac{1}{{1 + {\rm{j}}\cdot f/f_0 }}\quad\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \quad h_{\rm N}(t) = 2{\rm{\pi }}f_0 \cdot {\rm{e}}^{ - 2{\rm{\pi }}f_0 t} $$
Further, let it hold:
- Let the filter be optimally matched to the transmitted pulse shape $g(t)$ and the interference power-spectral density ${\it \Phi}_n (f)$, respectively:
- $$H(f) = H_{\rm MF}(f).$$
- The filter constant $K_{\rm MF}$ is to be chosen such that $H(f= 0) =1$.
- Let the detection time be $T_{\rm D}= 0$ for simplicity (acausal system description).
Notes:
- The chapter belongs to the chapter Matched Filter.
- In particular, we refer to the page Generalized matched filter for the case of colored interference.
- Given is the following definite integral:
- $$\frac{1}{{\sqrt {2{\rm{\pi }}} }}\int_{ - \infty }^{ + \infty } {x^2 \cdot {\rm e}^{ - x^2 /2} \,\,{\rm{d}}x} = 1.$$
Questions
Solution
- $$\rho_{d,\ \rm WR} = \frac{2E_g }{N_0 } = \frac{{2 \cdot 2.83 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}} {\rm{s}}}}{{10^{ - 6} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}}} = 5.66 \cdot 10^3 \quad \Rightarrow \quad 10\lg \cdot \rho _{d,\ \rm WR} \hspace{0.15cm}\underline {= 37.53\;{\rm{dB}}}.$$
(2) For the frequency response in the case of colored interferences, under the condition $T_{\rm D}= 0$:
- $$H_\text{MF} (f) = K_\text{MF}\cdot \frac{G^{\star} (f)}{\left| {H_{\rm N} (f)} \right|^2 }\hspace{0.2cm}{\rm with}\hspace{0.15cm} G(f) = g_0 \cdot \Delta t \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t \hspace{0.03cm}\cdot \hspace{0.03cm}f} \right)^2 } ,\hspace{0.15cm}\frac{1}{\left| {H_{\rm N} (f)} \right|^2 } =1+\left( f/f_0 \right)^2. $$
- From the condition $H_\text{MF}(f = 0) = 1$ it follows $K_\text{MF} = 1/(g_0 \cdot \Delta t)$. Thus one obtains:
- $$H_{\rm MF} (f) = {\rm{e}}^{ - {\rm{\pi }}[ {\Delta t \cdot f} ]^2 } \cdot \left( {1 + \left(f/f_0 \right)^2 } \right).$$
- For white (frequency-independent) noise, the matched filter would be given by the first term alone, which causes the matching to the pulse $g(t)$.
- For colored interference ⇒ PSD ${\it \Phi}_n(f)$, higher frequencies are raised by the correction term $1+\left( f/f_0 \right)^2$ because in this range the interference is lower.
- For $f = 1/\Delta t = 2f_0 = 1\hspace{0.08cm} \rm kHz$ we obtain:
- $$H_{\rm MF} ( {f = {1}/{\Delta t}} ) = {\rm{e}}^{ - {\rm{\pi }}} \cdot \left( {1 + 2^2 } \right) \hspace{0.15cm}\underline {= 0.216}.$$
(3) In general, the S/N ratio at the output of the matched filter is:
- $$\rho _d = \int_{ - \infty }^{ + \infty } {\frac{\left| {G(f)} \right|^2 }{\it{\Phi _n} \left( f \right)}\,\,{\rm{d}}f = } \int_{ - \infty }^{ + \infty } {\frac{\left| {G(f)} \right|^2 }{N_0 /2}} \, \,{\rm{d}}f \hspace{0.3cm}+ \hspace{0.3cm} \int_{ - \infty }^{ + \infty } {\frac{\left| {G(f)} \right|^2 }{N_0 /2}} \cdot \frac{f^2 }{f_0 ^2 }\,\,{\rm{d}}f.$$
- The first summand is equal to the S/N ratio withn white noise. For the second summand, we obtain:
- $$\Delta \rho _d = \frac{g_0 ^2 \cdot \Delta t^2 }{N_0 /2 \cdot f_0 ^2 }\cdot \int_{ - \infty }^{ + \infty } {f^2 \cdot {\rm{e}}^{ - 2{\rm{\pi }}\left( {f \cdot \Delta t} \right)^2 } }\,\, {\rm{d}}f.$$
- After substituting $x = 2 \cdot \pi^{0.5}\cdot f \cdot \Delta t$, this integral becomes:
- $$\Delta \rho _d = \frac{\sqrt 2 \cdot g_0 ^2 \cdot \Delta t}{N_0 } \cdot \frac{1}{{4{\rm{\pi }}\left( {\Delta t \cdot f_0 } \right)^2 }} \cdot \int_{ - \infty }^{ + \infty } {\frac{x^2 }{\sqrt {2{\rm{\pi }}} }} \cdot {\rm{e}}^{ - x^2 /2}\,\, {\rm{d}}x.$$
- This particular integral was given in the front; it has the value $1$. The first factor again describes the S/N ratio with white noise.
- This gives the following equations:
- $$\Delta \rho _d = \rho _{d,\rm WR} \cdot \frac{1}{{4{\rm{\pi }}\left( {\Delta t \cdot f_0 } \right)^2 }}, \hspace{1cm} \rho _d = \rho _{d,\rm WR} + \Delta \rho _d = \rho _{d, \rm WR} \left( {1 + \frac{1}{{4{\rm{\pi }}\left( {\Delta t \cdot f_0 } \right)^2 }}} \right).$$
- $$\Rightarrow \hspace{0.3cm} \Delta t \cdot f_0 = 0.5 : \hspace{0.3cm} \rho _d = 1.318 \cdot \rho _{d,\rm WR} = 7.46 \cdot 10^3 \hspace{0.3cm} \Rightarrow \quad 10\lg \rho _d \hspace{0.15cm}\underline {= 38.73\;{\rm{dB}}}.$$
Conclusion: There is a $1.2 \; \rm dB$ better result than with white noise, because ${\it \Phi}_n(f)$ is here smaller than $N_0/2$ in the whole frequency range except for the frequency $f = 0$ $($here the equal sign applies$)$. This fact is also used by the matched filter.