Further OFDM Applications

OFDM for DVB–T

$\rm DVB–T$ ("Digital Video Broadcasting Terrestrial") is one of several variants derived from the 1997 DVB standard for the distribution of television signals in digital form. Other related standards are:

$\rm DVB–S$ ⇒ for transmission via $\rm S\hspace{0.03cm}$atellite,
$\rm DVB–C$ ⇒ for transmission via the cable network $\rm (C\hspace{0.03cm}$able$)$,
$\rm DVB–H$ ⇒ for mobile devices $\rm (H\hspace{0.03cm}$andhelds$)$.

In Germany, more than $90\%$ of the population was already able to receive at least a selection of public broadcasters via DVB-T as of the end of 2008. Since 2017, analog TV reception via antenna has finally been no longer possible. The frequency bands freed up by the shutdown of analog transmission were directly reused by DVB-T, so that parallel operation and thus a "smooth transition" was not possible.

DVB-T uses the modulation method "Coded Orthogonal Frequency Division Multiplex" – abbreviated to $\rm COFDM$. The addition of "Forward Error Correction" $($ $\rm FEC)$ in combination with the guard interval technique already introduced is necessary to counteract interference caused by echoes ("multipath reception") and receiver movement ("Doppler effect").

Basically, DVB-T is a "common wave network". In contrast to conventional mobile communications networks – such as the GSM network – the same frequencies are reused even by directly adjacent transmitting stations. This leads to interference between similarly strong signals at the cell boundaries, which can, however, exhibit considerable differences in propagation time.

The effects of such a frequency-selective channel can be counteracted by extending the guard interval. However, on the one hand, this reduces the bandwidth efficiency, and it also increases the susceptibility to time-varying effects.

System parameters of DVB-T

The old analog television channels each had a bandwidth of

Parameters for DVB-T

$\text{7 MHz}$ $\rm (VHF$, "Very High Frequency" ⇒ "Ultra-short Wave$")$,
$\text{8 MHz}$ $\rm (UHF$, "Ultra High Frequency" ⇒ "Decimetric Wave"$)$.

In DVB-T, each of these channels is usually occupied by four programs. For this purpose, the available spectrum is divided among the OFDM subcarriers.

The table shows possible parameter constellations of a DVB-T system. "Mode" is the number of subcarriers used for FFT/IFFT, i.e. $\text{2048 (2K)}$ or $\text{8192 (8K)}$. However, not all carriers are actually used.

A comparison of the two modes shows that

the $\rm 2K$ mode is well suited for time-variant operating conditions because of the shorter core symbol duration $T$,
but due to the rather short guard interval duration $T_{\rm G}$, there are narrow limits to the tolerable channel impulse response.

In the $\rm 8K$ mode, this is exactly the opposite. Because of the requirement of a common wave network, 8K operation is therefore preferable to 2K operation, although the disadvantage of a more complex implementation of the FFT/IFFT must be accepted.

Three QAM variants are available for DVB-T subcarrier modulation:

$\rm 4–QAM$ (this method can also be understood as $\rm 4–PSK$ ),
$\rm 16–QAM$ (optionally with asymmetrical signal space constellation),
$\rm 64–QAM$ (also optionally with asymmetrical signal space constellation).

An asymmetrical signal space constellation allows hierarchical source coding. In poor transmission conditions, only the quadrant can be detected instead of the exact signal space point. Reception is thus still possible, albeit with (greatly) reduced image quality.

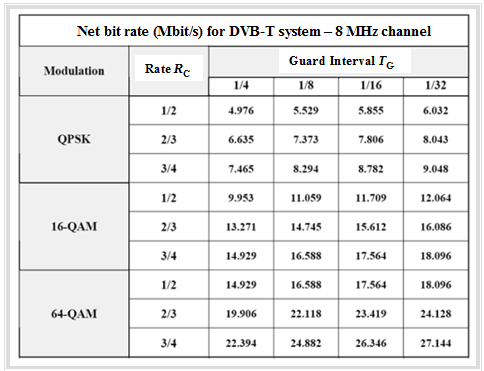
Net bit rates for DVB-T. Source: https://en.wikipedia.org/wiki/DVB-T#Technik

The table from WIKIPEDIA shows some resulting data rates for DVB-T depending on the channel coding rate $R_{\rm C}$ and the duration $T_{\rm G}$ of the guard interval. The relative code redundancy is $1 - R_{\rm C}$. This means that the larger the coding rate $R_{\rm C}$, the less redundancy is added.

The numerical values can be interpreted as follows:

The effective net bit rates vary greatly between individual transmission areas because different system parameters must be used depending on the region. On average, approximately $12$ ... $\text{20 Mbit/s}$ are achieved. This is now used to transmit an $\rm MPEG–2$ data stream, which usually contains four programs.

The video data streams for DVB-T in Germany are also MPEG-2 encoded and achieve a data rate of about $\text{3.5 Mbit/s}$. In comparison, a digitized PAL signal would already correspond to a data rate of $3$ ... $\text{5 Mbit/s},$ and DVD would already reach a data rate of approx. $\text{9.8 Mbit/s}$.

Since 2009, $\rm DVB–T2$ has been a standard that, among other things, uses $\rm MPEG–4$ instead of "MPEG–2". Compared to "DVB-T", the standard "DVB-T2" achieves a significantly better image quality.

A brief description of DSL - Digital Subscriber Line

As another example of the use of OFDM, a brief overview of $\rm DSL$ ("Digital Subscriber Line") will now be given:

DSL technology allows a considerable increase in data transmission rate compared to conventional telephone connections such as $\rm POTS$ ("Plain Old Telephone Service") or $\rm ISDN$ ("Integrated Services Digital Network"), without having to replace the copper pairs of the subscriber line for this new technology.
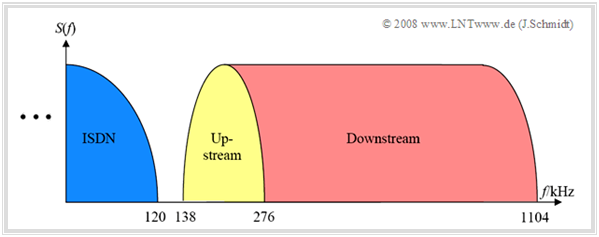
POTS or ISDN can also be operated in parallel with DSL without any restrictions, since the frequency bands used do not overlap if the appropriate adjustments are made (see diagram).

"Asymmetric Digital Subscriber Line" in an ISDN network

The following main xDSL variants exist
("x" is to be understood as a placeholder here):

$\rm ADSL$ ("Asymmetric Digital Subscriber Line"),
$\rm ADSL+$, an extension to ADSL,
$\rm VDSL/VDSL2$ ("Very High Data Rate Digital Subscriber Line").

VDSL2 is designed for maximum symmetrical data rates $($ $\text{210 Mbit/s}$ each upstream and downstream$)$, but can only be implemented over short lines.

OFDM is always used as the modulation method for all of these xDSL variants, which is often also called $\rm DMT$ ("Discrete Multitone Transmission") in this context.

We now consider DMT in ADSL with the following characteristics:

Base frequency $f_0 = 4.3125\ \rm kHz$,
maximum number of useful carriers: $N = 255$,
DC signal free, since $S(f = 0) = 0$,
the Nyquist tone ⇒ $S(256 · f_0)$ is also set to zero,
maximum frequency: $256 · 4.3125 \ \rm kHz = 1104 \ \rm kHz$.

This results in the spectrum occupancy shown in the figure. A detailed system description can be found in the chapter $\rm DSL$ of the LNTww book "Examples of Communication Systems".

The DSL spectrum shown can be described very briefly as follows:

The $224$ carriers available for DMT - these are often referred to as "bins" in the context of DMT – are used

either for "upstream" $($transmission into the network, $32$ bins, $\text{138 kHz)}$
or for "downstream" $($transmission out of the network, $192$ bins, $\text{828 kHz)}$.

All ADSL lines from "Deutsche Telekom" are switched according to the "ADSL-over-ISDN" standard, so that parallel operation with ISDN is possible. For this purpose, the frequency range up to $\text{138 kHz}$ is not used for ADSL and the corresponding bins are set to zero.
"ADSL-over-ISDN" and not "ADSL-over-POTS" is also used for analog connections, although this wastes precisely that frequency range which has a particularly favorable (low) cable attenuation.

The main advantage of DSL or DMT is again its adaptability to the channel. The copper twisted pairs used in the access network do not have an ideal attenuation and phase response, among other things, because of the skin effect. DMT again offers the possibility, depending on the quality of the frequency range of the bins, to adapt the respective modulation method or even to dispense with the use of a carrier altogether.

DSL also uses the guard interval technique in the form of the cyclic prefix. "Interleaving" can also be used to avoid errors, but this delays the transmission. The term "fast path" is used to describe the omission of this technique.

$\text{Conclusion:}$ In the field of wireline transmission technology, too,
it was only the transition from a single-carrier system to a multi-carrier system that enabled the high transmission rates common today.

Differences between DMT and the described OFDM

The OFDM system descriptions in the chapters "General Description of OFDM" as well as "Implementation of OFDM Systems" apply only to band-pass systems, which were always considered here in the equivalent low-pass range:

The low-pass transform removes all components at negative frequencies, resulting in an "unbalanced spectral function" and thus in a "complex-valued time signal".
This low-pass transformation is not necessary for DSL because, in contrast to mobile communications systems, it is operated in the baseband.

This leads to a different formula representation. For a clear distinction between the two approaches,

DMT spectrum

we will use "OFDM" in the following only for a band-pass system,
while the term "DMT" always refers to a baseband system.

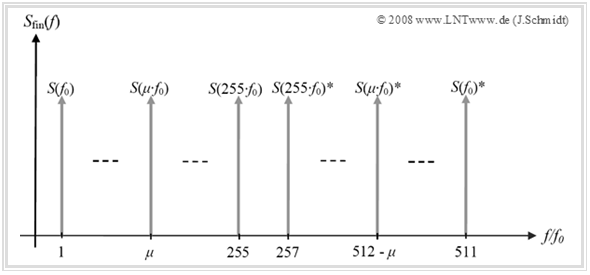
The diagram shows the spectrum of a DMT signal with $255$ used bins.

The useful carrier spectrum from $1$ to $255$ is supplemented by the corresponding negative frequency components to obtain a period of the "finite spectrum" required for IDFT, see [Han08]^[1]:

$$S(-\mu \cdot f_0 ) = S\big[(N - \mu ) \cdot f_0 \big] = S(\mu \cdot f_0)^*.$$

In general $0 < \mu < N/2$ and for the diagram $N = 512$.

According to the $\rm IDFT$, the thus purely "real time signal" at the sampling times $ν · T_{\rm A}$ with $0 ≤ ν < N$ and $T_{\rm A} = T/N$ results to:

$$s_\nu = \sum\limits_{\mu = 0}^{N - 1} {S(\mu \cdot f_0 ) \cdot {\rm{e}}^{{\kern 1pt} {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm}\nu \hspace{0.03cm}\cdot \hspace{0.03cm}\mu /{N}} }.$$

$\text{Conclusion:}$ The required number of frequency support points and samples of the $\rm IDFT/DFT$ corresponds to twice the usable carriers in the DMT method,

if the DC component as well as the "Nyquist tone" are neglected,
and is thus also twice as large as in an OFDM band-pass system.

$\text{Example 1:}$ Let $N = 512$ and $S(64 · f_0) = (a + {\rm j} · b)/2$ and $S(448 · f_0) = S^{\star}(64 · f_0) = (a - {\rm j} · b)/2$. Let all other spectral coefficients be zero.

(1) We now calculate the time domain coefficients using IDFT according to the given formula:

$$\begin{align*}s_\nu & = \sum\limits_{\mu = 0}^{N - 1} {S (\mu \cdot f_0 ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}\mu /{N} } } =S( 64 \cdot f_0 ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}64 /512} + S( 448 \cdot f_0 ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}448 /512} = \\ & = {1}/ {2} \cdot (a + {\rm{j} } \cdot b ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}64 /512} + {1}/{2} \cdot (a - {\rm{j} } \cdot b ) \cdot {\rm{e} }^{ {\rm{j \hspace{0.03cm}\cdot \hspace{0.03cm}2 \pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} \nu \hspace{0.03cm}\cdot \hspace{0.03cm}448 /512}.\end{align*}$$

(2) Applying $\text{Euler's theorem}$ to this, we get:

$$s_\nu = \frac{a + {\rm{j} } \cdot b } {2} \cdot \left[ {\rm{cos} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ) + {\rm{j} } \cdot {\rm{sin} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ) \right] + \frac{a - {\rm{j} } \cdot b } {2} \cdot \left[ {\rm{cos} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu ) + {\rm{j} } \cdot {\rm{sin} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu )\right],$$

where:

$${\rm{cos} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu ) = {\rm{cos} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ), \qquad {\rm{sin} } ( 2\pi \cdot \frac{ {448} } { {512} }\cdot \nu ) = - {\rm{sin} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ).$$

(3) Summarizing here yields purely real time signal coefficients:

$$s_\nu = a \cdot {\rm{cos} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ) - b \cdot {\rm{sin} } ( 2\pi \cdot \frac{ {64} } { {512} }\cdot \nu ).$$

The parameter $a$ represents the "in-phase component" of the QAM modulation of the respective carrier (bins).
The parameter $b$ indicates the "quadrature component".

The same procedure can be followed for the other "carrier pairs".

Exercise for the chapter

Exercise 5.10: DMT Process for DSL

References

↑ Hanik, N.: Leitungsgebundene Übertragungstechnik. Lecture manuscript. Lehrstuhl für Nachrichtentechnik, TU München, 2017.

[1] Hanik, N.: Leitungsgebundene Übertragungstechnik. Lecture manuscript. Lehrstuhl für Nachrichtentechnik, TU München, 2017.

[1]