Aufgaben:Exercise 4.6: Locality Curve for SSB-AM

• Return to book

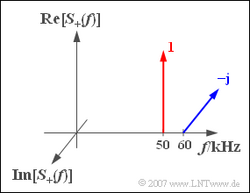
Wir betrachten das analytische Signal $s_+(t)$ mit der Spektralfunktion

$$S_{\rm +}(f) = 1 \cdot \delta (f - f_{\rm 50})- {\rm j} \cdot \delta (f - f_{\rm 60}) .$$

Hierbei stehen $f_{50}$ und $f_{60}$ als Abkürzungen für die Frequenzen 50 kHz bzw. 60 kHz.

In dieser Aufgabe soll der Verlauf des äquivalenten Tiefpass-Signals $s_{TP}(t)$ analysiert werden, das in diesem Tutorial auch als Ortskurve bezeichnet wird.

• In den Teilaufgaben (1) bis (3) gehen wir davon aus, dass das Signal $s(t)$ durch eine Einseitenband-Amplitudenmodulation des sinusförmigen Nachrichtensignals der Frequenz $f_{\rm N} = 10 \ \text{ kHz}$ mit cosinusförmigem Träger bei $f_{\rm T} = f_{50}$ entstanden ist, wobei nur das obere Seitenband (OSB) übertragen wird.
• Dagegen wird bei der Teilaufgabe (4) von der Trägerfrequenz $f_{\rm T} = f_{60}$ ausgegangen. Diese Annahme setzt voraus, dass eine USB-Modulation stattgefunden hat.

Hinweise:

• Die Aufgabe gehört zum Kapitel Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen:

Ortskurve – Darstellung des äquivalenten Tiefpass-Signals

Fragebogen

1

Geben Sie das äquivalente Tiefpass-Signal $s_{\rm TP}(t)$ für die Trägerfrequenz $f_{\rm N} = 10 \ \text{ kHz}$ an. Welche der folgenden Aussagen sind zutreffend?

	Die Ortskurve beschreibt eine Ellipse.
	Die Ortskurve beschreibt einen Kreis.
	Die Ortskurve beschreibt einen Kreisbogen.

2

Berechnen Sie die Betragsfunktion $a(t) = |s_{\rm TP}(t)|$. Wie groß ist der Wert $a_0$ bei $t = 0$ sowie der Maximal– und Minimalwert des Betrags?

$a_{\text{max}}$  =

$a_0$  =

$a_{\text{min}}$  =

3

Berechnen Sie die Phasenfunktion $\phi(t)$. Wie groß sind die Phasenwerte bei $t = 0$ sowie bei $t=25 \ \mu \text{s}$? Interpretieren Sie $\phi (t)$ im Bereich um $t=75 \ \mu \text{s}$.

$\phi(t=0 \ \mu \text{s})$  =  $\text{Grad}$

$\phi(t=25 \ \mu \text{s})$  =  $\text{Grad}$

$\phi(t=75 \ \mu \text{s})$  =  $\text{Grad}$

4

Geben Sie das äquivalente Tiefpass-Signal $s_{\rm TP}(t)$ für $f_{\rm T} = 60 \ \text{ kHz} = f_{60}$ an. Welche der folgenden Aussagen sind zutreffend?

	Die Ortskurve ist ein Kreis mit Radius $1$ um den Mittelpunkt $(0, –{\rm j})$ .
	Es gilt nun $s_{\rm TP}(t = 0) = 1 + {\rm j}$.
	Die Betragsfunktion $a(t)$ ist gegenüber $f_{\rm T} = f_{50}$ unverändert.
	Die Phasenfunktion $\phi (t)$ ist gegenüber $f_{\rm T} = f_{50}$ unverändert.

Musterlösung

Solution

1. Das Spektrum des äquivalenten TP–Signals lautet mit der Trägerfrequenz $f_{\rm T} = f_{50} = 50 \ \text{ kHz}$:

$$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 50}) = 1 \cdot \delta (f)- {\rm j} \cdot \delta (f - f_{\rm 10}) .$$

Damit ergibt sich für das dazugehörige Zeitsignal:

$$s_{\rm TP}(t) = {\rm 1 } - {\rm j} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$

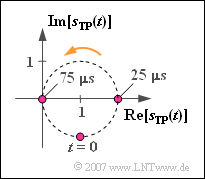
Ausgehend vom Punkt $(1, –{\rm j})$ verläuft $s_{\rm TP}(t)$ auf einem Kreis mit Mittelpunkt $(1, 0)$ und Radius $1$. Die Periodendauer ist gleich dem Kehrwert der Frequenz: $T_0 = 1/f_{10} = 100 \ \mu \text{s}$    ⇒    Antwort 2.

2. Spaltet man obige Gleichung nach Real- und Imaginäranteil auf, so erhält man:

$$s_{\rm TP}(t) = {\rm 1 } + \sin({ \omega_{\rm 10} \hspace{0.05cm} t }) -{\rm j}\cdot \cos({ \omega_{\rm 10} \hspace{0.05cm} t }).$$

Dies führt zur Betragsfunktion

$$\begin{align*}a(t)& = |s_{\rm TP}(t)|=\sqrt{{\rm Re}\left[s_{\rm TP}(t)\right]^2 + {\rm Im}\left[s_{\rm TP}(t)\right]^2 }= \\ & = \sqrt{1 + 2 \sin(\omega_{\rm 10}\hspace{0.05cm} t)+ \sin^2(\omega_{\rm 10}\hspace{0.05cm} t)+ \cos^2(\omega_{\rm 10}\hspace{0.05cm} t)} = \sqrt{2 \cdot ( 1 + \sin(\omega_{\rm 10}\hspace{0.05cm} t))}.\end{align*}$$

• Der Maximalwert ergibt sich aus sin( $\omega_{10} \cdot t \leq 1$ )    ⇒    $a_{\text{max}} \; \underline{= 2}$.
• Für den Minimalwert erhält man unter Berücksichtigung von $\sin(\omega_{10} \cdot t) \geq -1$    ⇒    $a_{\text{min}} \; \underline{= 0}$.
• Bei $t = 0$ ist der Betrag gleich $a_0 = \sqrt{2 }\; \underline{\approx 1.414}$.

3. Entsprechend der allgemeinen Definition gilt:

$$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm TP}(t)\right]}{{\rm Re}\left[s_{\rm TP}(t)\right]}= {\rm arctan} \hspace{0.1cm}\frac{-\cos(\omega_{\rm 10}\hspace{0.05cm} t)}{1 + \sin(\omega_{\rm 10}\hspace{0.05cm} t)}.$$

Für $t = 0$ ist $\cos( \omega_{10} \cdot t ) = 1$ und $\sin( \omega_{10} \cdot t ) = 0$. Daraus folgt:

$$\phi(t = 0)= {\rm arctan} (-1) \hspace{0.15 cm}\underline{= -45^\circ}.$$

Dagegen gilt für $t = T_0/4 =25 \ \mu \text{s}$ :

$$\cos(\omega_{\rm 10}\hspace{0.05cm} t) = 0; \hspace{0.2cm}\sin(\omega_{\rm 10}\hspace{0.05cm} t) = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = {\rm 25 \hspace{0.05cm} \mu s}) \hspace{0.15 cm}\underline{= 0}.$$

Die beiden bisher berechneten Winkel kann man auch aus obiger Grafik ablesen.

Der Phasenwert bei $t =75 \ \mu \text{s}$ muss dagegen durch Grenzübergang bestimmt werden, da hier sowohl der Real- als auch der Imaginärteil $0$ werden und somit das Argument der arctan–Funktion unbestimmt ist. Man erhält $\phi(t=75 \ \mu \text{s}) \; \underline{= 0}.$

Dieses Ergebnis soll hier numerisch nachgewiesen werden:

• Berechnet man die Phasenfunktion für $t =74 \ \mu \text{s}$, so erhält man mit $\omega_{10} \cdot t = 1.48 \cdot \pi \; \Rightarrow \; 266.4^\circ$:

$$\phi(t = {\rm 74 \hspace{0.05cm} \mu s})= {\rm arctan} \hspace{0.1cm}\frac{\cos(86.4^\circ)}{1 - \sin(86.4^\circ)} = {\rm arctan} \hspace{0.1cm}\frac{0.062}{1 - 0.998} \approx {\rm arctan}(31)\approx 88^\circ.$$

• Entsprechend gilt für $t =76 \ \mu \text{s}$ mit $\omega_{10} \cdot t = 1.52 \cdot \pi \; \Rightarrow \; 273.6^\circ$ :

$$\phi(t = {\rm 76 \hspace{0.05cm} \mu s})= {\rm arctan} \hspace{0.1cm}\frac{-\cos(86.4^\circ)}{1 - \sin(86.4^\circ)} \approx {\rm arctan}(-31)\approx -88^\circ.$$

• Diese Zahlenwerte lassen darauf schließen, dass die Grenzwerte für $t \; \rightarrow \; 75 \ \mu \text{s}$ sich zu $\pm 90^\circ$ ergeben, je nachdem, ob man sich diesem Wert von oben oder unten nähert.
• Der Phasenwert bei exakt $t =75 \ \mu \text{s}$ ist gleich dem Mittelwert zwischen rechts- und linksseitigem Grenzwert, also tzatsächlich $0$.

4. Mit der Trägerfrequenz $f_{\rm T} = f_{60} = 60 \ \text{ kHz}$ lauten die Gleichungen für Zeit– und Frequenzbereich:

$$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 60}) = -{\rm j} \cdot \delta (f) + \delta (f + f_{\rm 10}) ;$$

$$s_{\rm TP}(t) = - {\rm j} + 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$

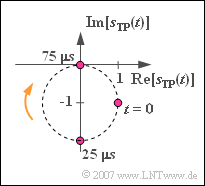
In der Grafik ist $s_{\rm TP}(t)$ dargestellt. Man erkennt:

• Die Ortskurve ist wiederum ein Kreis mit Radius $1$, aber nun mit Mittelpunkt $(0, –{\rm j})$.
• Es gilt auch hier $s_{\rm TP}(t = 0) = 1 – {\rm j}$.
• Man bewegt sich nun auf der Ortskurve im Uhrzeigersinn.
• Die Periodendauer beträgt weiterhin $T_0 = 1/f_{10} = 100 \ \mu \text{s}$.
• Die Ortskurve ist gegenüber drer Teiaufgabe (1) nur um $90^\circ$ in der komplexen Ebene gedreht. Für alle Zeiten ergeben sich die gleichen Zeigerlängen wie für $f_{\rm T} = f_{50}$. Der Betrag bleibt gleich.
• Die Phasenfunktion $\phi(t)$ liefert nun Werte zwischen $–\pi$ und $0$, während die in der Teilaufgabe (3) berechnete Phasenfunktion Werte zwischen $–\pi/2$ und $+\pi /2$ angenommen hat. Es gilt für alle Zeiten $t$::

$$\phi_{\rm Teilaufgabe(4)}= -(\phi_{\rm Teilaufgabe(3)} + 90^\circ).$$

Richtig sind somit der erste und der dritte Lösungsvorschlag.