Aufgaben:Exercise 1.2Z: Measurement of the Frequency Response

• Return to book

Z1.2 Messung von H(f)

Zur messtechnischen Bestimmung des Filterfrequenzgangs wird ein sinusförmiges Eingangssignal mit der Amplitude $2 \ \text{V}$ und vorgegebener Frequenz $f_0$ angelegt. Das Ausgangssignal $y(t)$ bzw. dessen Spektrum $Y(f)$ werden dann nach Betrag und Phase ermittelt.

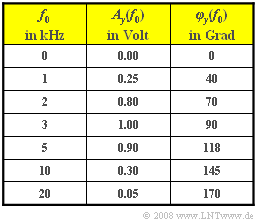
Das Betragsspektrum am Ausgang von Filter A lautet mit der Frequenz $f_0 = 1 \ \text{kHz}$: $$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ Bei einem anderen Filter B ist das Ausgangssignal dagegen stets eine harmonische Schwingung mit der (einzigen) Frequenz $f_0$. Bei den in der Tabelle angegebenen Frequenzen $f_0$ werden die Amplituden $A_y(f_0)$ und die Phasen $φ_y(f_0)$ gemessen. Hierbei gilt: $$Y_{\rm B} (f) = {A_y}/{2} \cdot {\rm e}^{ {\rm j} \varphi_y} \cdot {\rm \delta } (f + f_0) + {A_y}/{2} \cdot {\rm e}^{ -{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$ Das Filter B soll in der Aufgabe in der Form $$H_{\rm B}(f) = {\rm e}^{-a_{\rm B}(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_{\rm B}(f)}$$

dargestellt werden. Hierbei bezeichnet

• $a_{\rm B}(f)$ den Dämpfungsverlauf, und
• $b_{\rm B}(f)$ den Phasenverlauf.

Hinweise:

• Die Aufgabe gehört zum Kapitel Systembeschreibung im Frequenzbereich.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der Aussagen sind hinsichtlich des Filters A zutreffend?

	Es gilt $|H(f)| = 0.8$.
	Das Filter A stellt kein LZI–System dar.
	Die Angabe eines Frequenzgangs ist nicht möglich.

2

Welche der Aussagen sind hinsichtlich des Filters B zutreffend?

	Filter B ist ein Tiefpass.
	Filter B ist ein Hochpass.
	Filter B ist ein Bandpass.
	Filter B ist eine Bandsperre.

3

Ermitteln Sie den Dämpfungswert und die Phase für $f_0 = 3 \ \text{kHz}$.

$a_{\rm B}(f_0 = \: \rm 3 \: kHz) \ =$  $\text{Np}$

$b_{\rm B}(f_0 = \: \rm 3 \: kHz) \ =$  $\text{Grad}$

4

Welcher Dämpfungs– und Phasenwert ergibt sich für $f_0 = 2 \ \text{kHz}$?

$a_{\rm B}(f_0 = \: \rm 2 \: kHz) \ = $  $\text{Np}$

$b_{\rm B}(f_0 = \: \rm 2 \: kHz) \ =$  $\text{Grad}$

Musterlösung

Solution

1. Bei einem LZI–System gilt $Y(f) = X(f) · H(f)$. Daher ist es nicht möglich, dass im Ausgangssignal ein Anteil mit $3 f_0$ vorhanden ist, wenn ein solcher im Eingangssignal fehlt. Das heißt: Es liegt hier kein LZI–System vor und dementsprechend ist auch kein Frequenzgang angebbar. Richtig sind demnach die Lösungsvorschläge 2 und 3.

2. Aufgrund der angegeben Zahlenwerte für $A_y(f_0)$ kann von einem Bandpass ausgegangen werden.

3. Mit $A_x = 2 \ \text{ V}$ und $varphi_x = 90^\circ$ (Sinusfunktion) erhält man für $f_0 = f_3 =3 \ \text{ kHz}$: $$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} (\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - 90^{\circ})} = 0.5.$$ Somit ergeben sich für $f_0 = f_3 = 3 \ \text{ kHz}$ die Werte

• $a_{\rm B} (f_3)\rm \underline{\: ≈ \: 0.693 \: Np}$,
• $b_{\rm B}(f_3) \rm \underline{\: = \: 0 \: (Grad)}$.

4. In analoger Weise kann der Frequenzgang bei $f_0 = f_2 =2 \ \text{ kHz}$ ermittelt werden: $$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - 70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$ Damit erhält man für $f_0 = f_2 = 2 \ \text{ kHz}$:

• $a_{\rm B}(f_2) \rm \underline{\: ≈ \: 0.916 \: Np}$,
• $b_{\rm B}(f_2) \rm \underline{\: = \: 20°}$.

Bei $f_0 = -f_2 =-\hspace{-0.01cm}2 \ \text{ kHz}$ gilt der gleiche Dämpfungswert. Die Phase hat jedoch das umgekehrte Vorzeichen. Also ist $b_{\rm B}(–f_2) = \ –\hspace{-0.01cm}20^{\circ}.$