Difference between revisions of "Aufgaben:Exercise 2.1: Linear? Or Non-Linear?"
m (Guenter verschob die Seite 2.1 Linear - Nichtlinear nach 2.1 Linear? - Nichtlinear?) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID879__LZI_A_2_1.png|right|]] | [[File:P_ID879__LZI_A_2_1.png|right|]] | ||
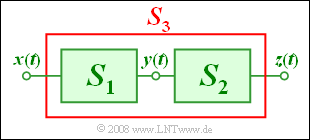
| − | + | Wir betrachten die skizzierte Anordnung mit dem Eingangssignal $x(t)$ und dem Ausgangssignal $z(t)$: | |
| − | + | Das System $S_1(t)$ ist durch folgende Gleichung beschreibbar: | |
| − | + | $$y(t) = x(t) + {1 \, \rm V}^{\rm -1} \cdot x^2(t) .$$ | |
| − | + | Über das System <i>S</i><sub>2</sub> mit Eingangssignal <i>y</i>(<i>t</i>) und Ausgangssignal <i>z</i>(<i>t</i>) ist nichts weiter bekannt. | |
| − | + | Das System <i>S</i><sub>3</sub> ist die Zusammenschaltung von <i>S</i><sub>1</sub> und <i>S</i><sub>2</sub>. | |
| − | + | An den Eingang wird folgendes Signal angelegt (<i>f</i><sub>0</sub> = 5 kHz): | |
| − | + | $$x(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) .$$ | |
| − | + | Damit erhält man am Ausgang des Gesamtsystems <i>S</i><sub>3</sub>: | |
| − | + | $$z(t) = {1 \, \rm V} \cdot {\rm sin}(2\pi f_0 t ) .$$ | |
| − | + | <b>Hinweis:</b> Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.1. Gegeben ist die folgende trigonometrische Beziehung: | |
| − | + | $$\cos^2(\alpha) = \frac{1}{2} \cdot \left[ 1 + \cos(2\alpha)\right] | |
.$$ | .$$ | ||
Revision as of 10:19, 1 February 2017
Wir betrachten die skizzierte Anordnung mit dem Eingangssignal $x(t)$ und dem Ausgangssignal $z(t)$:
Das System $S_1(t)$ ist durch folgende Gleichung beschreibbar: $$y(t) = x(t) + {1 \, \rm V}^{\rm -1} \cdot x^2(t) .$$
Über das System S2 mit Eingangssignal y(t) und Ausgangssignal z(t) ist nichts weiter bekannt.
Das System S3 ist die Zusammenschaltung von S1 und S2.
An den Eingang wird folgendes Signal angelegt (f0 = 5 kHz): $$x(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) .$$
Damit erhält man am Ausgang des Gesamtsystems S3: $$z(t) = {1 \, \rm V} \cdot {\rm sin}(2\pi f_0 t ) .$$
Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.1. Gegeben ist die folgende trigonometrische Beziehung: $$\cos^2(\alpha) = \frac{1}{2} \cdot \left[ 1 + \cos(2\alpha)\right] .$$
Fragebogen
Musterlösung
- 1. Aufgrund der Kennlinie mit linearem und quadratischem Anteil gilt:
- $$y(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) + {1 \, \rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 t ) \\ = {2 \, \rm V} \cdot \left[ 1 + {\rm cos}(2\pi f_0 t ) +{\rm cos}(4\pi f_0 t ) \right].$$
- Zum Zeitpunkt t = 0 tritt somit der Signalwert 6 V auf.
- 2. Ein ideales System kommt wegen z(t) ≠ x(t) nicht in Frage. Die Alternativen 2 und 3 sind möglich. Bei nur einer Frequenz (f0 = 5 kHz) ist keine Aussage möglich, ob eine zweite Frequenzkomponente ebenfalls um α = 0.5 gedämpft und um τ = T0/4 = 50 μs verzögert würde. Die letzte Alternative müsste der Beobachter – obwohl teilweise zutreffend – logischerweise verneinen.
- 3. Er würde erkennen, dass S2 ein linear verzerrendes System ist ⇒ Lösungsvorschlag 2. Bei einem verzerrungsfreien System müsste z(t) zusätzlich noch eine Gleich– und eine 10 kHz–Komponente beinhalten, bei einem nichtlinear verzerrenden System noch größere Frequenzanteile (bei Vielfachen von 10 kHz).
- 4. In diesem Fall würde Y(f) Spektrallinien bei f = 0, f = 10 kHz und f = 20 kHz aufweisen. Die auf der Angabenseite beschriebene Messung mit f0 = 5 kHz hat gezeigt, dass H2(f = 0) und H2(f = 10 kHz) jeweils 0 sein werden. Die einzig mögliche Signalform ist somit
- $$z(t) = {2 \, \rm V} \cdot H_2 (f = {20 \, \rm kHz})\cdot {\rm cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$
- Möglich sind also die erste und die letzte der genannten Alternativen, je nachdem, ob das System S2 die Frequenz 20 kHz unterdrückt oder durchlässt ⇒ Lösungsvorschläge 1 und 3.