Difference between revisions of "Aufgaben:Exercise 4.3: Operational Attenuation"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige Ergebnisse der Leitungstheorie }} right| :Wird eine Nachricht…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
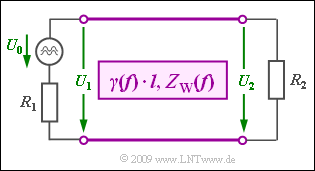
| − | [[File:P_ID1800__LZI_A_4_3.png|right|]] | + | [[File:P_ID1800__LZI_A_4_3.png|right|Betrachtetes Leitungsmodell]] |
| − | + | Wird eine Nachrichtenverbindung der Länge $l$ nicht an beiden Enden mit ihrem Wellenwiderstand $Z_{\rm W}$ abgeschlossen, so kommt es stets zu Reflexionen. Anstelle der Wellendämpfung $a_{\rm W} = \alpha \cdot l$ muss man in diesem Fall die Betriebsdämpfung $a_{\rm B}$ betrachten, die hier ohne Frequenzabhängigkeit angegeben wird. Das heißt: wir betrachten hier stets nur eine einzige Frequenz $f_0$: | |
| − | + | $${ a}_{\rm B} = { a}_{\rm B}(f_0)= { a}_{\rm W}+ {\rm ln}\hspace{0.1cm} |q_1|+{\rm ln}\hspace{0.1cm} |q_2|+{ a}_{\rm WWD}\hspace{0.05cm}.$$ | |
| − | + | Die vier Anteile – alle mit der Pseudoeinheit „Neper (Np)” – beschreiben folgende Sachverhalte: | |
| − | + | * Der erste Summand $a_{\rm W} = \alpha \cdot l$ modelliert die '''Wellendämpfung''' der sich entlang der Leitung ausbreitenden Welle. Beachten Sie, dass Dämpfungen mit „$a$” bezeichnet werden, während das Dämpfungsmaß (kilometrische Dämpfung) mit „$\alpha$” ⇒ sprich: „alpha” gekennzeichnetist. | |
| − | + | * Der zweite Summand gibt die '''senderseitige Stoßdämpfung''' an. Dieser Term berücksichtigt den Leistungsverlust durch Reflexionen am Übergang „Sender–Leitung”: | |
| − | |||
| − | |||
:$${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} | :$${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | * In analoger Weise gilt für die '''empfängerseitige Stoßdämpfung''' am Leitungsende ⇒ Übergang „Leitung–Empfänger”: | |
| − | |||
:$${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} | :$${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | * Die '''Wechselwirkungsdämpfung''' beschreibt die Signaldämpfung durch die Auswirkung einer doppelt reflektierten Welle, die sich dem Nutzsignal konstruktiv oder destruktiv überlagern kann. Für diesen letzten Anteil | |
| − | + | :$${ a}_{\rm WWD} = {\rm ln}\hspace{0.1cm} |1- r_1 \cdot r_2 \cdot {\rm e}^{- 2\hspace{0.05cm}\cdot\hspace{0.05cm} | |
| − | :$${ | ||
\gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$ | \gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$ | ||
:verwenden wir in dieser Aufgabe folgende Gleichungen und Nomenklatur: | :verwenden wir in dieser Aufgabe folgende Gleichungen und Nomenklatur: | ||
| − | :$${ | + | :$${a}_{\rm WWD} = {\rm ln}\hspace{0.1cm}A, \hspace{0.3cm}A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \hspace{0.05cm}\cdot\hspace{0.05cm} |
\beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| | \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 30: | Line 26: | ||
\hspace{0.3cm}r_2= \frac {R_2 - Z_{\rm W}}{R_2 + Z_{\rm W}} | \hspace{0.3cm}r_2= \frac {R_2 - Z_{\rm W}}{R_2 + Z_{\rm W}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | : | + | |
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie|Einige Ergebnisse der Leitungstheorie]]. | ||
| + | *Wesentliche Informationen finden Sie auf der Seite [[Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie#Einfluss_von_Reflexionen_.E2.80.93_Betriebsd.C3.A4mpfung|Einfluss von Reflexionen - Betriebsdämpfung]] | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Gehen Sie bei numerischen Berechnungen von folgenden Zahlenwerten aus: | ||
:$$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} | :$$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} | ||
R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} | R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} | ||
| Line 41: | Line 42: | ||
{Welcher Wert ergäbe sich für die Betriebsdämpfung, wenn es keine Reflexionen geben würde? | {Welcher Wert ergäbe sich für die Betriebsdämpfung, wenn es keine Reflexionen geben würde? | ||
|type="{}"} | |type="{}"} | ||
| − | $Anpassung:\ a_B$ | + | ${\rm bei \; Anpassung}\hspace{-0.1cm}:\ a_B \ =$ { 0.2 3% } $\ \rm Np$ |
| − | {Berechnen Sie die beiden Anteile der Stoßdämpfung für | + | {Berechnen Sie die beiden Anteile der Stoßdämpfung für $Z_{\rm W} = 100\,{\rm \Omega}$ sowie $R_1 = 200\,{\rm \Omega}$ und $ R_2 = 1\,{\rm k\Omega}$. |
|type="{}"} | |type="{}"} | ||
| − | $ln\ |q_1|$ | + | $ln\ |q_1| \ =$ { 0.059 3% } $\ \rm Np$ |
| − | $ln\ |q_2|$ | + | $ln\ |q_2| \ =$ { 0.553 3% } $\ \rm Np$ |
| − | {Berechnen Sie die Reflexionsfaktoren | + | {Berechnen Sie die Reflexionsfaktoren $r_1$, $r_2$ und $r_\alpha$. |
|type="{}"} | |type="{}"} | ||
| − | $r_1$ | + | $r_1 \ =$ { 0.333 3% } |
| − | $r_2$ | + | $r_2\ =$ { 0.818 3% } |
| − | $r_\alpha$ | + | $r_\alpha\ =$ { 0.183 3% } |
| − | {Welche Bedingung muss die | + | {Welche Bedingung muss die Hilfsgröße $A$ erfüllen, damit es zu konstruktiver bzw. destruktiver Überlagerung bezüglich der Wechselwirkungsdämpfung kommt? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $A$ ist minimal ⇒ konstruktive Überlagerung, |
| − | + | + | + $A$ ist maximal ⇒ destruktive Überlagerung. |
| − | {Geben Sie den kleinstmöglichen Wert | + | {Geben Sie den kleinstmöglichen Wert $\beta_\text{min}$ für das Phasenmaß $\beta(f_0)$ an, damit es zu einer konstruktiven Überlagerung kommt. |
|type="{}"} | |type="{}"} | ||
| − | $\beta_\text{min}$ | + | $\beta_\text{min} \ =$ { 0.785 3% } $\ \rm rad/km$ |
{Wie groß kann der Wechselwirkungsdämpfungsanteil maximal werden? Welche Voraussetzungen müssen hierfür gelten? | {Wie groß kann der Wechselwirkungsdämpfungsanteil maximal werden? Welche Voraussetzungen müssen hierfür gelten? | ||
|type="{}"} | |type="{}"} | ||
| − | $Max\ [a_\text{WWD}]$ | + | ${\rm Max}\ [a_\text{WWD}] \ =$ { 0.693 3% } $\ \rm Np$ |
Revision as of 10:20, 15 February 2017
Wird eine Nachrichtenverbindung der Länge $l$ nicht an beiden Enden mit ihrem Wellenwiderstand $Z_{\rm W}$ abgeschlossen, so kommt es stets zu Reflexionen. Anstelle der Wellendämpfung $a_{\rm W} = \alpha \cdot l$ muss man in diesem Fall die Betriebsdämpfung $a_{\rm B}$ betrachten, die hier ohne Frequenzabhängigkeit angegeben wird. Das heißt: wir betrachten hier stets nur eine einzige Frequenz $f_0$: $${ a}_{\rm B} = { a}_{\rm B}(f_0)= { a}_{\rm W}+ {\rm ln}\hspace{0.1cm} |q_1|+{\rm ln}\hspace{0.1cm} |q_2|+{ a}_{\rm WWD}\hspace{0.05cm}.$$ Die vier Anteile – alle mit der Pseudoeinheit „Neper (Np)” – beschreiben folgende Sachverhalte:
- Der erste Summand $a_{\rm W} = \alpha \cdot l$ modelliert die Wellendämpfung der sich entlang der Leitung ausbreitenden Welle. Beachten Sie, dass Dämpfungen mit „$a$” bezeichnet werden, während das Dämpfungsmaß (kilometrische Dämpfung) mit „$\alpha$” ⇒ sprich: „alpha” gekennzeichnetist.
- Der zweite Summand gibt die senderseitige Stoßdämpfung an. Dieser Term berücksichtigt den Leistungsverlust durch Reflexionen am Übergang „Sender–Leitung”:
- $${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} \hspace{0.05cm}.$$
- In analoger Weise gilt für die empfängerseitige Stoßdämpfung am Leitungsende ⇒ Übergang „Leitung–Empfänger”:
- $${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} \hspace{0.05cm}.$$
- Die Wechselwirkungsdämpfung beschreibt die Signaldämpfung durch die Auswirkung einer doppelt reflektierten Welle, die sich dem Nutzsignal konstruktiv oder destruktiv überlagern kann. Für diesen letzten Anteil
- $${ a}_{\rm WWD} = {\rm ln}\hspace{0.1cm} |1- r_1 \cdot r_2 \cdot {\rm e}^{- 2\hspace{0.05cm}\cdot\hspace{0.05cm} \gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$
- verwenden wir in dieser Aufgabe folgende Gleichungen und Nomenklatur:
- $${a}_{\rm WWD} = {\rm ln}\hspace{0.1cm}A, \hspace{0.3cm}A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| \hspace{0.05cm},$$
- $$r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} \alpha \hspace{0.05cm}\cdot\hspace{0.05cm} l},\hspace{0.3cm}r_1= \frac {R_1 - Z_{\rm W}}{R_1 + Z_{\rm W}}, \hspace{0.3cm}r_2= \frac {R_2 - Z_{\rm W}}{R_2 + Z_{\rm W}} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Ergebnisse der Leitungstheorie.
- Wesentliche Informationen finden Sie auf der Seite Einfluss von Reflexionen - Betriebsdämpfung
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Gehen Sie bei numerischen Berechnungen von folgenden Zahlenwerten aus:
- $$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} \alpha = 0.1\,{\rm Np/km} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- 1. Bei Widerstandsanpassung (R1 = R2 = ZW) verbleibt von den vier Summanden nur der erste:
- $${\rm a}_{\rm B} = \alpha \cdot l = 0.1\,{\rm Np/km} \cdot 2\,{\rm km} \hspace{0.15cm}\underline{= 0.2\,{\rm Np}}\hspace{0.05cm}.$$
- 2. Entsprechend den angegebenen Gleichungen ergibt sich:
- $$q_1 = \frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}}= \frac {200 + 100}{2 \cdot \sqrt{200 \cdot 100}}= 1.061 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} {\rm ln}\hspace{0.1cm}|q_1| \hspace{0.15cm}\underline{= 0.059 \,{\rm Np}} \hspace{0.05cm},\\ q_2 = \frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}}= \frac {1000 + 100}{2 \cdot \sqrt{1000 \cdot 100}}= 1.739 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} {\rm ln}\hspace{0.1cm}|q_2| \hspace{0.15cm}\underline{= 0.553 \,{\rm Np}}\hspace{0.05cm}.$$
- 3. Mit den vorgegebenen Beschaltungswiderständen erhält man
- $$r_1= \frac {200\,{\rm \Omega} - 100\,{\rm \Omega}}{200\,{\rm \Omega} + 100\,{\rm \Omega}} \hspace{0.15cm}\underline{= 0.333}\hspace{0.05cm}, \hspace{0.3cm}\frac {1000\,{\rm \Omega} - 100\,{\rm \Omega}}{1000\,{\rm \Omega} + 100\,{\rm \Omega}}\hspace{0.15cm}\underline{ = 0.818}$$
- $$\Rightarrow \hspace{0.3cm} r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} \alpha \hspace{0.05cm}\cdot\hspace{0.05cm} l}= 0.333 \cdot 0.818\cdot {\rm e}^{-4}\hspace{0.15cm}\underline{= 0.183} \hspace{0.05cm}.$$
- 4. Beide Aussagen sind richtig: Bei konstruktiver Überlagerung ist aWWD = ln A negativ ⇒ A < 1 und minimal. Im Gegensatz dazu bewirkt der maximale Wert von A (für den A > 1 gilt) eine positive Wechselwirkungsdämpfung, also eine zusätzliche Dämpfung des Nutzsignals aufgrund der destruktiven Überlagerung von hin– und rücklaufender Welle.
- 5. In der letzten Teilaufgabe wurde gezeigt, dass konstruktive Überlagerung gleichbedeutend ist mit der Minimierung von
- $$A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}|= |1- r_\alpha \cdot \cos(2 \beta l)+ {\rm j} \cdot \sin(2 \beta l)|=\\ = \sqrt {1- 2 \cdot r_\alpha \cdot \cos(2 \beta l)+ {r_\alpha}^2 \cdot \cos^2(2 \beta l)+ {r_\alpha}^2 \cdot \sin^2(2 \beta l)}=\\ = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)} \hspace{0.05cm}.$$
- Das Minimum ergibt sich für
- $$\cos(2 \beta l) = +1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta l= \pi, 2\pi, 3\pi, ... \hspace{0.2cm}\Rightarrow \hspace{0.2cm}\beta_{\rm min} = \frac{\pi}{2l}\hspace{0.15cm}\underline{= 0.785\,{\rm rad/km}} \hspace{0.05cm}.$$
- Dagegen kommt es zu destruktiver Überlagerung, falls das Phasenmaß folgende Bedingung erfüllt:
- $$\cos(2 \beta l) = -1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta l= \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, ...$$
- 6. Das Argument
- $$A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)}$$
- kann maximal A = 2 ⇒ aWWD = 0.693 Np werden unter folgenden Voraussetzungen:
- nicht abgeschlossene Leitung (r1 = r2 = 1),
- kurze Kabellänge, so dass der Term α · l nicht wirksam ist (rα = 1),
- Phasenverlauf entsprechend Teilaufgabe 5).