Aufgaben:Exercise 4.3: Operational Attenuation

• Return to book

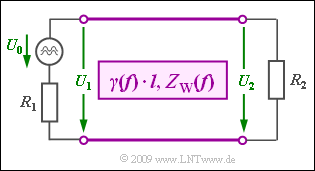
Wird eine Nachrichtenverbindung der Länge $l$ nicht an beiden Enden mit ihrem Wellenwiderstand $Z_{\rm W}$ abgeschlossen, so kommt es stets zu Reflexionen. Anstelle der Wellendämpfung $a_{\rm W} = \alpha \cdot l$ muss man in diesem Fall die Betriebsdämpfung $a_{\rm B}$ betrachten, die hier ohne Frequenzabhängigkeit angegeben wird. Das heißt: wir betrachten hier stets nur eine einzige Frequenz $f_0$: $${ a}_{\rm B} = { a}_{\rm B}(f_0)= { a}_{\rm W}+ {\rm ln}\hspace{0.1cm} |q_1|+{\rm ln}\hspace{0.1cm} |q_2|+{ a}_{\rm WWD}\hspace{0.05cm}.$$ Die vier Anteile – alle mit der Pseudoeinheit „Neper (Np)” – beschreiben folgende Sachverhalte:

• Der erste Summand $a_{\rm W} = \alpha \cdot l$ modelliert die Wellendämpfung der sich entlang der Leitung ausbreitenden Welle. Beachten Sie, dass Dämpfungen mit „$a$” bezeichnet werden, während das Dämpfungsmaß (kilometrische Dämpfung) mit „$\alpha$”   ⇒   sprich: „alpha” gekennzeichnetist.
• Der zweite Summand gibt die senderseitige Stoßdämpfung an. Dieser Term berücksichtigt den Leistungsverlust durch Reflexionen am Übergang „Sender–Leitung”:

$${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} \hspace{0.05cm}.$$

• In analoger Weise gilt für die empfängerseitige Stoßdämpfung am Leitungsende   ⇒   Übergang „Leitung–Empfänger”:

$${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} \hspace{0.05cm}.$$

• Die Wechselwirkungsdämpfung beschreibt die Signaldämpfung durch die Auswirkung einer doppelt reflektierten Welle, die sich dem Nutzsignal konstruktiv oder destruktiv überlagern kann. Für diesen letzten Anteil

$${ a}_{\rm WWD} = {\rm ln}\hspace{0.1cm} |1- r_1 \cdot r_2 \cdot {\rm e}^{- 2\hspace{0.05cm}\cdot\hspace{0.05cm} \gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$

verwenden wir in dieser Aufgabe folgende Gleichungen und Nomenklatur:

$${a}_{\rm WWD} = {\rm ln}\hspace{0.1cm}A, \hspace{0.3cm}A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| \hspace{0.05cm},$$

$$r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} \alpha \hspace{0.05cm}\cdot\hspace{0.05cm} l},\hspace{0.3cm}r_1= \frac {R_1 - Z_{\rm W}}{R_1 + Z_{\rm W}}, \hspace{0.3cm}r_2= \frac {R_2 - Z_{\rm W}}{R_2 + Z_{\rm W}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Einige Ergebnisse der Leitungstheorie.
• Wesentliche Informationen finden Sie auf der Seite Einfluss von Reflexionen - Betriebsdämpfung
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gehen Sie bei numerischen Berechnungen von folgenden Zahlenwerten aus:

$$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} \alpha = 0.1\,{\rm Np/km} \hspace{0.05cm}.$$

Fragebogen

1

Welcher Wert ergäbe sich für die Betriebsdämpfung, wenn es keine Reflexionen geben würde?

${\rm bei \; Anpassung}\hspace{-0.1cm}:\ a_{\rm B} \ =$ $\ \rm Np$

2

Berechnen Sie die beiden Anteile der Stoßdämpfung für $Z_{\rm W} = 100\,{\rm \Omega}$ sowie $R_1 = 200\,{\rm \Omega}$ und $ R_2 = 1\,{\rm k\Omega}$.

$ln\ |q_1| \ =$ $\ \rm Np$

$ln\ |q_2| \ =$ $\ \rm Np$

3

Berechnen Sie die Reflexionsfaktoren $r_1$, $r_2$ und $r_\alpha$.

$r_1 \ =$

$r_2\ =$

$r_\alpha\ =$

4

Welche Bedingung muss die Hilfsgröße $A$ erfüllen, damit es zu konstruktiver bzw. destruktiver Überlagerung bezüglich der Wechselwirkungsdämpfung kommt?

	$A$ ist minimal  ⇒  konstruktive Überlagerung,
	$A$ ist maximal  ⇒  destruktive Überlagerung.

5

Geben Sie den kleinstmöglichen Wert $\beta_\text{min}$ für das Phasenmaß $\beta(f_0)$ an, damit es zu einer konstruktiven Überlagerung kommt.

$\beta_\text{min} \ =$ $\ \rm rad/km$

6

Wie groß kann der Wechselwirkungsdämpfungsanteil maximal werden? Welche Voraussetzungen müssen hierfür gelten?

${\rm Max}\ [a_\text{WWD}] \ =$ $\ \rm Np$

Musterlösung

Solution

(1)  Bei Widerstandsanpassung ($R_1 = R_2 =Z_{\rm W}$) verbleibt von den vier Summanden nur der erste: $${\rm a}_{\rm B} = \alpha \cdot l = 0.1\,{\rm Np/km} \cdot 2\,{\rm km} \hspace{0.15cm}\underline{= 0.2\,{\rm Np}}\hspace{0.05cm}.$$

(2)  Entsprechend den angegebenen Gleichungen ergibt sich: $$q_1 = \frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}}= \frac {200 + 100}{2 \cdot \sqrt{200 \cdot 100}}= 1.061 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} {\rm ln}\hspace{0.1cm}|q_1| \hspace{0.15cm}\underline{= 0.059 \,{\rm Np}} \hspace{0.05cm},$$ $$q_2 = \frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}}= \frac {1000 + 100}{2 \cdot \sqrt{1000 \cdot 100}}= 1.739 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} {\rm ln}\hspace{0.1cm}|q_2| \hspace{0.15cm}\underline{= 0.553 \,{\rm Np}}\hspace{0.05cm}.$$

(3)  Mit den vorgegebenen Beschaltungswiderständen erhält man $$r_1= \frac {200\,{\rm \Omega} - 100\,{\rm \Omega}}{200\,{\rm \Omega} + 100\,{\rm \Omega}} \hspace{0.15cm}\underline{= 0.333}\hspace{0.05cm}, \hspace{0.3cm}\frac {1000\,{\rm \Omega} - 100\,{\rm \Omega}}{1000\,{\rm \Omega} + 100\,{\rm \Omega}}\hspace{0.15cm}\underline{ = 0.818}$$ $$\Rightarrow \hspace{0.3cm} r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} \alpha \hspace{0.05cm}\cdot\hspace{0.05cm} l}= 0.333 \cdot 0.818\cdot {\rm e}^{-4}\hspace{0.15cm}\underline{= 0.183} \hspace{0.05cm}.$$

(4)  Beide Aussagen sind richtig:

• Bei konstruktiver Überlagerung ist ${a}_{\rm WWD} = {\rm ln}\hspace{0.1cm}A < 0 \; \Rightarrow \; A < 1$ und minimal.
• Im Gegensatz dazu bewirkt der maximale Wert von $A$ (für den $A > 1$ gilt) eine positive Wechselwirkungsdämpfung, also eine zusätzliche Dämpfung des Nutzsignals aufgrund der destruktiven Überlagerung von hin– und rücklaufender Welle.

(5)  In der letzten Teilaufgabe wurde gezeigt, dass konstruktive Überlagerung gleichbedeutend ist mit der Minimierung von $$A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}|= |1- r_\alpha \cdot \cos(2 \beta l)+ {\rm j} \cdot \sin(2 \beta l)| = \sqrt {1- 2 \cdot r_\alpha \cdot \cos(2 \beta l)+ {r_\alpha}^2 \cdot \cos^2(2 \beta l)+ {r_\alpha}^2 \cdot \sin^2(2 \beta l)}$$ $$ \Rightarrow \hspace{0.3cm }A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)} \hspace{0.05cm}.$$ Das Minimum ergibt sich für $$\cos(2 \beta l) = +1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta l= \pi, 2\pi, 3\pi, ... \hspace{0.2cm}\Rightarrow \hspace{0.2cm}\beta_{\rm min} = {\pi}({2l})\hspace{0.15cm}\underline{= 0.785\,{\rm rad/km}} \hspace{0.05cm}.$$ Dagegen kommt es zu destruktiver Überlagerung, falls das Phasenmaß folgende Bedingung erfüllt: $$\cos(2 \beta l) = -1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta l= {\pi}/{2}, {3\pi}/{2}, {5\pi}/{2}, ...$$

(6)  Das Argument $A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)}$ kann maximal $A = 2$   ⇒   ${\rm Max}\ [a_\text{WWD}] \; \underline {= 0.693 \ \rm Np}$ werden unter folgenden Voraussetzungen:

• nicht abgeschlossene Leitung ($r_1 = r_2 = 1$),
• kurze Kabellänge, so dass der Term $\alpha \cdot l$ nicht wirksam ist ($r_\alpha = 1$),
• Phasenverlauf entsprechend der Teilaufgabe (5).