Difference between revisions of "Aufgaben:Exercise 2.2: Multi-Level Signals"
| Line 43: | Line 43: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Man erhält durch Mittelung über alle möglichen Signalwerte für den linearen Mittelwert: | |
| − | + | $$m_{\it x}=\rm \sum_{\mu=0}^{\it M-{\rm 1}} \it p_\mu\cdot x_{\mu}=\frac{\rm 1}{\it M} \cdot \sum_{\mu=\rm 0}^{\it M-\rm 1}\mu=\frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M}{\rm 2}=\frac{\it M-\rm 1}{\rm 2}.$$ | |
| − | + | Im Sonderfall $M= 5$ ergibt sich der lineare Mittelwert zu $m_x \;\underline{= 2}$. | |
| − | + | '''(2)''' Analog gilt für den quadratischen Mittelwert: | |
| − | + | $$m_{\rm 2\it x}= \rm \sum_{\mu=0}^{\it M -\rm 1}\it p_\mu\cdot x_{\mu}^{\rm 2}=\frac{\rm 1}{\it M}\cdot \sum_{\mu=\rm 0}^{\rm M-1}\mu^{\rm 2} = \frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M\cdot(\rm 2\it M-\rm 1)}{\rm 6} = \frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}.$$ | |
| − | + | Im Sonderfall $M= 5$ ergibt sich der quadratische Mittelwert zu $m_{2x} {=6}$. Daraus kann die Varianz mit dem Satz von Steiner berechnet werden: | |
| + | $$\sigma_x^{\rm 2}=m_{\rm 2\it x}-m_x^{\rm 2}=\frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}-\frac{(\it M-\rm 1)^{\rm 2}}{\rm 4}=\frac{\it M^{\rm 2}-\rm 1}{\rm 12}.$$ | ||
| − | + | Im Sonderfall $M= 5$ ergibt sich für die Varianz $\sigma_x^2 \;\underline{= 2}$. | |
| − | |||
| − | : | + | '''(3)''' Aufgrund der Symmetrie von $y$ gilt unabhängig von $M$: $m_x \;\underline{= 2}$. |
| − | |||
| − | |||
| − | + | '''(4)''' Zwischen $x(t)$ und $y(t)$ gilt folgender Zusammenhang: | |
| − | + | $$y(t)=\frac{2\cdot y_{\rm 0}}{M-\rm 1}\cdot [x(t)-m_x].$$ | |
| − | + | Daraus folgt für die Varianzen: | |
| − | + | $$\sigma_y^{\rm 2}=\frac{4\cdot y_{\rm 0}^{\rm 2}}{( M - 1)^{\rm 2}}\cdot \sigma_x^{\rm 2}=\frac{y_{\rm 0}^{\rm 2}\cdot (M^{\rm 2}-1)}{3\cdot (M- 1)^{\rm 2}}=\frac{y_{\rm 0}^{\rm 2}\cdot ( M+ 1)}{ 3\cdot ( M- 1)}.$$ | |
| − | + | Im Sonderfall $M= 5$ ergibt sich hierfür: | |
| − | + | $$\it \sigma_y^{\rm 2}= \frac {\it y_{\rm 0}^{\rm 2} \cdot {\rm 6}}{\rm 3 \cdot 4}\hspace{0.15cm} \underline{=\rm2\,V^{2}}.$$ | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 14:41, 2 March 2017
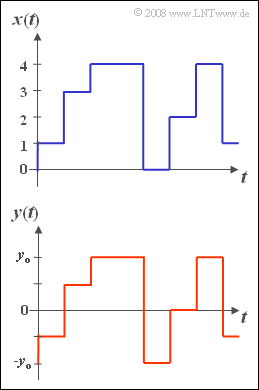
Das Rechtecksignal $x(t)$ sei dimensionslos und kann nur die Momentanwerte $0, 1, 2, ... , M-2, M-1$ mit gleicher Wahrscheinlichkeit annehmen. Die obere Grafik zeigt dieses Signal für den Sonderfall $M = 5$.
Auch das Rechtecksignal $y(t)$ sei$M$–stufig, aber mittelwertfrei und auf den Wertebereich von $y > -y_0$ bis $y < +y_0$ beschränkt. In der unteren Grafik sehen Sie das Signal $y(t)$, wiederum für die Stufenzahl $M = 5$. Setzen Sie für numerische Berechnungen $y_0 = 2\hspace{0.05cm}V$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Momente einer diskreten Zufallsgröße.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Eine Zusammenfassung der Theamatik bietet das folgende Lernvideo:
Fragebogen
Musterlösung
Im Sonderfall $M= 5$ ergibt sich der lineare Mittelwert zu $m_x \;\underline{= 2}$.
(2) Analog gilt für den quadratischen Mittelwert: $$m_{\rm 2\it x}= \rm \sum_{\mu=0}^{\it M -\rm 1}\it p_\mu\cdot x_{\mu}^{\rm 2}=\frac{\rm 1}{\it M}\cdot \sum_{\mu=\rm 0}^{\rm M-1}\mu^{\rm 2} = \frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M\cdot(\rm 2\it M-\rm 1)}{\rm 6} = \frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}.$$
Im Sonderfall $M= 5$ ergibt sich der quadratische Mittelwert zu $m_{2x} {=6}$. Daraus kann die Varianz mit dem Satz von Steiner berechnet werden: $$\sigma_x^{\rm 2}=m_{\rm 2\it x}-m_x^{\rm 2}=\frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}-\frac{(\it M-\rm 1)^{\rm 2}}{\rm 4}=\frac{\it M^{\rm 2}-\rm 1}{\rm 12}.$$
Im Sonderfall $M= 5$ ergibt sich für die Varianz $\sigma_x^2 \;\underline{= 2}$.
(3) Aufgrund der Symmetrie von $y$ gilt unabhängig von $M$: $m_x \;\underline{= 2}$.
(4) Zwischen $x(t)$ und $y(t)$ gilt folgender Zusammenhang:
$$y(t)=\frac{2\cdot y_{\rm 0}}{M-\rm 1}\cdot [x(t)-m_x].$$
Daraus folgt für die Varianzen: $$\sigma_y^{\rm 2}=\frac{4\cdot y_{\rm 0}^{\rm 2}}{( M - 1)^{\rm 2}}\cdot \sigma_x^{\rm 2}=\frac{y_{\rm 0}^{\rm 2}\cdot (M^{\rm 2}-1)}{3\cdot (M- 1)^{\rm 2}}=\frac{y_{\rm 0}^{\rm 2}\cdot ( M+ 1)}{ 3\cdot ( M- 1)}.$$
Im Sonderfall $M= 5$ ergibt sich hierfür: $$\it \sigma_y^{\rm 2}= \frac {\it y_{\rm 0}^{\rm 2} \cdot {\rm 6}}{\rm 3 \cdot 4}\hspace{0.15cm} \underline{=\rm2\,V^{2}}.$$