Difference between revisions of "Theory of Stochastic Signals/Binomial Distribution"
| Line 29: | Line 29: | ||
Für die '''Wahrscheinlichkeiten der Binomialverteilung''' gilt mit $μ = 0, ... , I$: | Für die '''Wahrscheinlichkeiten der Binomialverteilung''' gilt mit $μ = 0, ... , I$: | ||
$$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ | $$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ | ||
| − | Der erste Term gibt hierbei die Anzahl der Kombinationen („$I$ über $μ$”) an: | + | Der erste Term gibt hierbei die Anzahl der Kombinationen („$I$ '''über''' $μ$”) an: |
$${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$ | $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$ | ||
{{end}} | {{end}} | ||
| Line 56: | Line 56: | ||
| − | == | + | ==Blockfehlerwahrscheinlichkeit== |
| + | Ein weiteres Beispiel für die Anwendung der Binomialverteilung ist die Berechnung der Blockfehlerwahrscheinlichkeit bei einem digitalen Übertragungssystem. | ||
| + | |||
{{Beispiel}} | {{Beispiel}} | ||
| − | Überträgt man jeweils Blöcke von $I =$ | + | Überträgt man jeweils Blöcke von $I =10$ Binärsymbolen über einen Kanal, der |
| + | *mit der Wahrscheinlichkeit $p = 0.01$ ein Symbol verfälscht ⇒ Zufallsgröße $e_i = 1$, und | ||
| + | *entsprechend mit der Wahrscheinlichkeit $1 – p = 0.99$ das Symbol unverfälscht überträgt ⇒ Zufallsgröße $e_i = 0$, | ||
| + | so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”): | ||
$$f=\sum_{i=1}^{I}e_i.$$ | $$f=\sum_{i=1}^{I}e_i.$$ | ||
| − | Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen 0 (kein Symbol verfälscht) und $I$ (alle Symbole falsch) annehmen | + | Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $0$ (kein Symbol verfälscht) und $I$ (alle Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ$. |
| − | *Der Fall, dass alle $I$ Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.99^{10} ≈ 0.9044$ ein. Dies ergibt sich auch aus der Binomialformel für $μ =$ | + | *Der Fall, dass alle $I$ Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.99^{10} ≈ 0.9044$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition „10 über 0“ = 1. |
*Ein einziger Symbolfehler $(f = 1)$ tritt mit folgender Wahrscheinlichkeit auf: | *Ein einziger Symbolfehler $(f = 1)$ tritt mit folgender Wahrscheinlichkeit auf: | ||
| − | $$p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$$ | + | :$$p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$$ |
| − | Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau „10 über 1“ = 10 Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und neun richtig übertragen werden müssen, wenn $f =$ | + | Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau „10 über 1“ = $10$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und neun richtig übertragen werden müssen, wenn $f =1$ gelten soll. |
| − | *Für $f =$ | + | *Für $f =2$ gibt es deutlich mehr Kombinationen, nämlich „10 über 2“ = $45$, und man erhält |
| − | $$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$ | + | :$$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$ |
Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit | Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit | ||
| Line 78: | Line 83: | ||
==Momente der Binomialverteilung== | ==Momente der Binomialverteilung== | ||
| − | Die Momente können mit den Gleichungen | + | Die Momente können mit den Gleichungen im Kapitel [[Stochastische_Signaltheorie/Momente_einer_diskreten_Zufallsgröße|Momente einer diskreten Zufallsgröße]] und den Wahrscheinlichkeiten der Binomialverteilung allgemein berechnet werden. |
| + | |||
| + | Für das '''Moment $k$-ter Ordnung''' gilt: | ||
$$m_k=\rm E[\it z^k \rm ]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ | $$m_k=\rm E[\it z^k \rm ]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ | ||
Revision as of 13:47, 3 March 2017
Contents
Allgemeine Beschreibung der Binomialverteilung
Die Binomialverteilung stellt einen wichtigen Sonderfall für die Auftrittswahrscheinlichkeiten einer diskreten Zufallsgröße dar.
Zur Herleitung der Binomialverteilung gehen wir davon aus, dass $I$ binäre und statistisch voneinander unabhängige Zufallsgrößen $b_i$
- den Wert $1$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 1) = p$, und
- den Wert $0$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 0) = 1-p$ annehmen kann.
Dann ist die Summe $z$ ebenfalls eine diskrete Zufallsgröße mit dem Symbolvorrat $\{0, 1, 2, ... , I\}$, die man als binomialverteilt bezeichnet:
- $$z=\sum_{i=1}^{I}b_i.$$
Der Symbolumfang beträgt somit $M = I + 1.$
Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen:
- Sie beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle.
- Sie erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung.
- Auch die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist eigentlich eine binomialverteilte Zufallsgröße.
Wahrscheinlichkeiten der Binomialverteilung
Für die Wahrscheinlichkeiten der Binomialverteilung gilt mit $μ = 0, ... , I$: $$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ Der erste Term gibt hierbei die Anzahl der Kombinationen („$I$ über $μ$”) an: $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$
Weitere Hinweise:
- Für sehr große Werte von $I$ kann die Binomialverteilung durch die im nächsten Abschnitt beschriebene Poissonverteilung angenähert werden.
- Ist gleichzeitig das Produkt $I · p \gg 1$, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über.
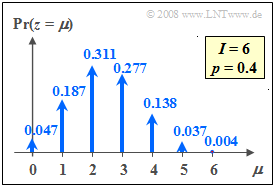Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung sind für $I =6$ und $p =0.4$. Von Null verschieden sind somit $M = I+1=7$ Wahrscheinlichkeiten.
Dagegen ergeben sich für $I = 6$ und $p = 0.5$ die folgenden Binomialwahrscheinlichkeiten: $$\begin{align*}{\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}0) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}6)\hspace{-0.05cm} =\hspace{-0.05cm} 1/64\hspace{-0.05cm} = \hspace{-0.05cm}0.015625 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}1) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}5) \hspace{-0.05cm}= \hspace{-0.05cm}6/64 \hspace{-0.05cm}=\hspace{-0.05cm} 0.09375,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}2) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}4)\hspace{-0.05cm} = \hspace{-0.05cm}15/64 \hspace{-0.05cm}= \hspace{-0.05cm}0.234375 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}3) & = 20/64 \hspace{-0.05cm}= \hspace{-0.05cm} 0.3125 .\end{align*}$$
Diese sind symmetrisch bezüglich des Abszissenwertes $\mu = I/2$.
Mit nachfolgendem Berechnungsmodul können Sie die Binomialwahrscheinlichkeiten auch für andere Parameterwerte $I$ und $p$ ermitteln:
Ereigniswahrscheinlichkeiten der Binomialverteilung
Blockfehlerwahrscheinlichkeit
Ein weiteres Beispiel für die Anwendung der Binomialverteilung ist die Berechnung der Blockfehlerwahrscheinlichkeit bei einem digitalen Übertragungssystem.
Überträgt man jeweils Blöcke von $I =10$ Binärsymbolen über einen Kanal, der
- mit der Wahrscheinlichkeit $p = 0.01$ ein Symbol verfälscht ⇒ Zufallsgröße $e_i = 1$, und
- entsprechend mit der Wahrscheinlichkeit $1 – p = 0.99$ das Symbol unverfälscht überträgt ⇒ Zufallsgröße $e_i = 0$,
so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”): $$f=\sum_{i=1}^{I}e_i.$$
Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $0$ (kein Symbol verfälscht) und $I$ (alle Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ$.
- Der Fall, dass alle $I$ Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.99^{10} ≈ 0.9044$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition „10 über 0“ = 1.
- Ein einziger Symbolfehler $(f = 1)$ tritt mit folgender Wahrscheinlichkeit auf:
- $$p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$$
Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau „10 über 1“ = $10$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und neun richtig übertragen werden müssen, wenn $f =1$ gelten soll.
- Für $f =2$ gibt es deutlich mehr Kombinationen, nämlich „10 über 2“ = $45$, und man erhält
- $$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$
Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit $$p_{\rm R} = \it p_{\rm 3} \rm +... \rm + \it p_{\rm 10}\approx \rm 10^{-4},$$ oder $$p_{\rm R} = \rm 1-\it p_{\rm 0}-\it p_{\rm 1}-p_{\rm 2}\approx \rm 10^{-4}.$$
Man erkennt, dass die zweite Berechnungsmöglichkeit über das Komplement schneller zum Ziel führt. Man könnte aber auch berücksichtigen, dass bei diesen Zahlenwerten $p_{\rm R} ≈ p_3$ gilt.
Momente der Binomialverteilung
Die Momente können mit den Gleichungen im Kapitel Momente einer diskreten Zufallsgröße und den Wahrscheinlichkeiten der Binomialverteilung allgemein berechnet werden.
Für das Moment $k$-ter Ordnung gilt: $$m_k=\rm E[\it z^k \rm ]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$
Daraus erhält man nach einigen Umformungen für
- den linearen Mittelwert:
$$m_1 = I\cdot p,$$
- den quadratischen Mittelwert:
$$m_2 = (I^2-I)\cdot p^2+I\cdot p.$$ Die Varianz und die Streuung erhält man durch Anwendung des Steinerschen Satzes: $$\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$$
Die maximale Varianz $σ_2 = I/4$ ergibt sich für die charakteristische Wahrscheinlichkeit $p =$ 1/2. In diesem Fall sind die Wahrscheinlichkeit symmetrisch um den Mittelwert $m_1 = I/2 ⇒ p_μ = p_{I–μ}$.
Je mehr die charakteristische Wahrscheinlichkeit $p$ vom Wert 1/2 abweicht,
- um so kleiner ist die Streuung $σ$, und
- um so unsymmetrischer werden die Wahrscheinlichkeiten um den Mittelwert $m_1 = I · p$.
Wir betrachten wie im letzten Beispiel einen Block von $I =$ 10 Symbolen, die jeweils mit der Wahrscheinlichkeit $p =$ 0.01 unabhängig voneinander verfälscht werden. Dann ist
- ist die mittlere Anzahl von Fehlern pro Block gleich $m_f =$ E[ $f$] $= I · p =$ 0.1, und
- die Streuung (Standardabweichung) der Zufallsgröße $f$ beträgt $σ_f ≈$ 0.315.
Im vollständig gestörten Kanal ⇒ charakteristische Wahrscheinlichkeit $p =$ 1/2 ergeben sich demgegenüber die Werte $m_f =$ 5 und $σ_f ≈$ 1.581.
Aufgaben zum Kapitel
Aufgabe 2.3: Mehrstufensignale
Zusatzaufgabe 2.3Z: Diskrete Zufallsgrößen
