Aufgaben:Exercise 3.3Z: Moments for Triangular PDF

• Return to book

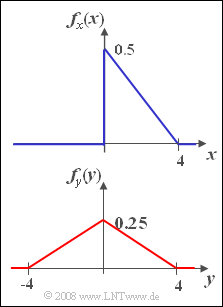
Wir betrachten in dieser Aufgabe zwei Zufallssignale $x(t)$ und $y(t)$ mit jeweils dreieckförmiger WDF, nämlich die

• einseitige Dreieck-WDFgemäß der oberen Grafik:

$$f_x(x)=\left\{ \begin{array}{*{4}{c}} 0.5 \cdot (1-{ x}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.1cm}{\rm 0 \le {\it x} \le 4},\\\rm 0 & \rm sonst. \end{array} \right.$$

• zweiseitige Dreieck-WDF gemäß der unteren Grafik:

$$ f_y(y)=\left\{ \begin{array}{*{4}{c}} 0.25 \cdot (1-{ |y|}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.1cm}{ -4 \le {\it y} \le \rm 4},\\\rm 0 & \rm sonst. \end{array} \right.$$

Berücksichtigen Sie zur Lösung dieser Aufgabe die Gleichung für die Zentralmomente: $$\mu_k=\sum\limits_{\kappa = \rm 0}^{\it k}\left({k} \atop {\kappa}\right)\cdot m_k\cdot(-m_{\rm 1})^{k - \kappa}.$$

Im Einzelnen ergeben sich mit dieser Gleichung folgende Ergebnisse: $$\mu_{\rm 1}=0,\hspace{0.5cm}\mu_{\rm 2}=\it m_{\rm 2}-\it m_{\rm 1}^{\rm 2},\hspace{0.5cm}\mu_{\rm 3}=\it m_{\rm 3}-\rm 3\cdot\it m_{\rm 2}\cdot \it m_{\rm 1} {\rm +}\rm 2\cdot\it m_{\rm 1}^{\rm 3},$$ $$\mu_{\rm 4}=\it m_{\rm 4}-\rm 4\cdot\it m_{\rm 3}\cdot \it m_{\rm 1}\rm +6\cdot\it m_{\rm 2}\cdot\it m_{\rm 1}^{\rm 2}-\rm 3\cdot\it m_{\rm 1}^{\rm 4}.$$

Aus den Zentralmomenten höherer Ordnung kann man unter anderem ableiten:

• die Charliersche Schiefe $S = {\mu_3}/{\sigma^3}\hspace{0.05cm},$

• die Kurtosis $K = {\mu_4}/{\sigma^4}\hspace{0.05cm}.$

Hinweise:

• Die Aufgabe gehört zum Kapitel Erwartungswerte und Momente.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie aus der vorliegenden WDF $f_x(x)$ das Moment $k$-ter Ordnung. Welcher Wert ergibt sich für den linearen Mittelwert $m_x = m_1$?

$m_x \ =$

2

Wie groß sind der quadratische Mittelwert und die Streuung $\sigma_x$ der Zufallsgröße $x$?

$\sigma_x\ =$

3

Wie groß ist bei der Zufallsgröße $x$ die Charliersche Schiefe $S_x = \mu_3/\sigma_x^3$? Warum ist $S_x \ne 0$?

$S_x \ =$

4

Welche Aussagen treffen für die symmetrisch verteilte Zufallsgröße $y$ zu?

	Alle Momente mit ungeradzahligem $k$ sind $m_k =0$.
	Alle Momente mit geradzahligem $k$ sind $m_k =0$.
	Alle Momente $m_k$ mit geradzahligem $k$ sind wie in der Teilaufgabe (1) berechnet.
	Die Zentralmomente $\mu_k$ sind gleich den Momenten $m_k$.

5

Berechnen Sie die Streuung der Zufallsgröße $y$.

$\sigma_y \ =$

6

Welcher Wert ergibt sich für die Kurtosis $K_y$ der Zufallsgröße $y$? Interpretieren Sie das Ergebnis.

$K_y \ =$

Musterlösung

Solution

(1)  Für das Moment $k$–ter Ordnung der Zufallsgröße $x$ gilt: $$m_k=1/2\cdot \int_{\rm 0}^{\rm 4} x^k\cdot ( 1-\frac{\it x}{\rm 4}) \hspace{0.1cm}{\rm d}x.$$

Dies führt zu dem Ergebnis: $$m_k=\frac{x^{ k+ 1}}{ 2\cdot ( k+ 1)}\Bigg|_{\rm 0}^{\rm 4}-\frac{x^{ k+2}}{8\cdot ( k+2)}\Bigg|_{\rm 0}^{\rm 4}=\frac{\rm 2\cdot \rm 4^{\it k}}{(\it k\rm +1)\cdot (\it k\rm + 2)}.$$

Daraus erhält man für den linearen Mittelwert ($k= 1$): $$m_x=\rm {4}/{3}\hspace{0.15cm}\underline{=1.333}.$$

(2)  Der quadratische Mittelwert ($k= 2$) beträgt $m_2 = 8/3$. Daraus folgt mit dem Satz von Steiner: $$\sigma_x^{\rm 2}={8}/{3}-({4}/{3})^2=\rm {8}/{9}\hspace{0.5cm}\Rightarrow\hspace{0.5cm} \sigma_x\hspace{0.15cm}\underline{\approx \rm 0.943}.$$

(3)  Mit $m_1 = 4/3$, $m_2 = 8/3$ und $m_3 = 32/5$ erhält man mit der angegebenen Gleichung für das Zentralmoment dritter Ordnung: $\mu_3 = 64/135 \approx 0.474$. Daraus folgt für die Charliersche Schiefe: $$S_x=\rm \frac{64/135}{\Big(\sqrt {8/9}\Big)^3}=\frac{\sqrt{8}}{5}\hspace{0.15cm}\underline{\approx 0.566}.$$

Aufgrund der unsymmetrischen WDF ist $S_x \ne 0$.

(4)  Richtig sind die Lösungsvorschläge 1, 3 und 4:

• Bei symmetrischer WDF sind alle ungeraden Momente $0$, unter anderem auch der Mittelwert $m_y$. Deshalb gibt es hinsichtlich der Zufallsgröße $y$> keinen Unterschied zwischen den Momenten $m_k$ und den Zentralmomenten $\mu_k$.
• Die Momente $m_k$ mit geradzahligem $k$ sind für die Zufallsgrößen $x$ und $y$ gleich. Offensichtlich wird dies an den Zeitmittelwerten. Da $x^2(t) = y^2(t)$, sind für $k = 2n$ auch die Momente gleich:

$$m_k=m_{2 n}=...\int [x^2(t)]^n \hspace{0.1cm}{\rm d} x=...\int [y^2(t)]^n \hspace{0.1cm}{\rm d} y.$$

(5)  Mit dem Ergebnis der Teilaufgabe (2) gilt: $$m_2=\mu_{\rm 2}=\sigma_y^2=\rm {8}/{3} = 2.667\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_y\hspace{0.15cm}\underline{=1.633}.$$

(6)  Das Zentralmoment vierter Ordnung ist bei symmetrischer WDF gleich dem Moment $m_4$. Aus der in Teilaufgabe (1) berechneten allgemeinen Gleichung erhält man $\mu_4 = 256/15.$ Daraus folgt für die Kurtosis: $$K_y=\frac{\mu_{\rm 4}}{\sigma_y^{\rm 4}}=\rm \frac{256/15}{(8/3)^2}\hspace{0.15cm}\underline{=2.4}.$$

Dieser Zahlenwert gilt für die Dreieck-WDF allgemein und liegt zwischen den Kurtosiswerten von Gleichverteilung ($K = 1.8$) und Gaußverteilung ($K = 3$). Dies ist eine quantitative Bewertung der Tatsache, dass hier die Ausläufer ausgeprägter sind als bei einer gleichverteilten Zufallsgröße, aber aufgrund der Begrenzung weniger stark als bei Gaußschen Größen.

Anschließend soll noch nachgewiesen werden, dass auch die unsymmetrische Dreieck-WDF $f_x(x)$ entsprechend der oberen Skizze auf dem Angabenblatt die gleiche Kurtosis besitzt: $$\mu_{ 4} = m_{\rm 4}- 4\cdot m_{\rm 3}\cdot m_{\rm 1}+ 6\cdot m_{\rm 2}\cdot m_{\rm 1}^{\rm 2}- 3\cdot m_{\rm 1}^{\rm 4}= \frac{256}{15} - 4 \cdot \frac{32}{5}\cdot \frac{4}{3} + 6 \cdot \frac{8}{3}\cdot \left(\frac{4}{3}\right)^2 -3 \cdot \left(\frac{4}{3}\right)^4 =\frac{256}{15 \cdot 9}$$

Mit dem Ergebnis der Teilaufgabe (3)  ⇒  $\sigma_x^2 = 8/9$ folgt daraus: $$ K_x = \frac{{256}/(15 \cdot 9)}{8/9 \cdot 8/9} = 2.4.$$