Difference between revisions of "Aufgaben:Exercise 5.5Z: Complexity of the FFT"
From LNTwww
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1179__Sig_Z_5_5.png|right]] | + | [[File:P_ID1179__Sig_Z_5_5.png|right|Zum Rechenaufwand der FFT]] |
| − | Der FFT–Algorithmus realisiert eine Diskrete Fouriertransformation mit dem kleinstmöglichen Rechenaufwand, wenn der Parameter | + | Der FFT–Algorithmus realisiert eine Diskrete Fouriertransformation mit dem kleinstmöglichen Rechenaufwand, wenn der Parameter $N$ eine Zweierpotenz ist. Im Einzelnen sind zur Durchführung einer FFT folgende Rechenschritte notwendig: |
| − | + | *Die FFT geschieht in ${\rm ld} \ N$ Stufen, wobei in jeder Stufe die genau gleiche Anzahl an Rechenoperationen durchzuführen ist. „ld” steht hier als Abkürzung für den Logarithmus zur Basis 2. | |
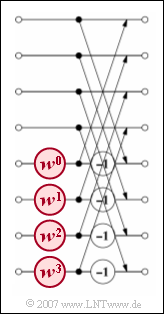
| + | *Die Grafik zeigt die dritte und letzte Stufe für das Beispiel $N = 8$. Man erkennt, dass in dieser und auch den anderen Stufen jeweils $N/2$ Basisoperationen durchzuführen sind. | ||
| + | *In jeder Basisoperation, die man häufig auch als '''Butterfly''' bezeichnet, werden aus den beiden komplexen Eingangsgrößen $E_1$ und $E_2$ zwei komplexe Ausgänge berechnet: | ||
| + | :$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$ | ||
| + | :$$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$ | ||
| + | *Hierbei bezeichnet $w = {\rm e}^{-{\rm j} 2\pi/N}$ den komplexen Drehfaktor. Für das Beispiel $N = 8$ hat dieser folgenden Wert: $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/4} = \cos(45^\circ) - {\rm j} \cdot \sin(45^\circ)\hspace{0.05cm}.$ | ||
| + | *Der Exponent $\mu$ dieses komplexen Drehfaktors kann alle ganzzahligen Werte zwischen $0$ und $N/2-1$ annehmen. Für $N = 8$ gilt: | ||
| + | :$$w^0 = 1,\hspace{0.2cm}w^1 = {1}/{\sqrt{2}}- {\rm j} | ||
| + | \cdot{1}/{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm | ||
| + | j},\hspace{0.2cm}w^3 = -{1}/{\sqrt{2}}- {\rm j} | ||
| + | \cdot{1}/{\sqrt{2}} \hspace{0.05cm}.$$ | ||
| − | + | Mit dieser Aufgabe sollen die für die FFT erforderliche Anzahl von Rechenoperationen $(O_{\rm FFT})$ ermittelt und mit dem für die DFT angebbaren Wert $O_{\rm DFT} ≈ 8\cdot N^2$ verglichen werden. | |
| − | : | + | Zu beachten ist: |
| − | |||
| − | |||
| − | + | *Sinnvollerweise werden die Potenzen von $w$ vor dem eigentlichen Algorithmus berechnet und in einer Lookup–Tabelle abgelegt. Die hierfür notwendigen Operationen sollen deshalb unberücksichtigt bleiben. | |
| − | $w | + | *Die Bitumkehroperation – eine Umsortierung, die vor der ersten Stufe durchzuführen ist – soll bei dieser Abschätzung ebenfalls nicht berücksichtigt werden. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Hinweise:'' | |
| + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fast-Fouriertransformation_(FFT)|Fast-Fouriertransformation (FFT)]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 11:27, 4 April 2017
Der FFT–Algorithmus realisiert eine Diskrete Fouriertransformation mit dem kleinstmöglichen Rechenaufwand, wenn der Parameter $N$ eine Zweierpotenz ist. Im Einzelnen sind zur Durchführung einer FFT folgende Rechenschritte notwendig:
- Die FFT geschieht in ${\rm ld} \ N$ Stufen, wobei in jeder Stufe die genau gleiche Anzahl an Rechenoperationen durchzuführen ist. „ld” steht hier als Abkürzung für den Logarithmus zur Basis 2.
- Die Grafik zeigt die dritte und letzte Stufe für das Beispiel $N = 8$. Man erkennt, dass in dieser und auch den anderen Stufen jeweils $N/2$ Basisoperationen durchzuführen sind.
- In jeder Basisoperation, die man häufig auch als Butterfly bezeichnet, werden aus den beiden komplexen Eingangsgrößen $E_1$ und $E_2$ zwei komplexe Ausgänge berechnet:
- $$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$
- $$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$
- Hierbei bezeichnet $w = {\rm e}^{-{\rm j} 2\pi/N}$ den komplexen Drehfaktor. Für das Beispiel $N = 8$ hat dieser folgenden Wert: $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/4} = \cos(45^\circ) - {\rm j} \cdot \sin(45^\circ)\hspace{0.05cm}.$
- Der Exponent $\mu$ dieses komplexen Drehfaktors kann alle ganzzahligen Werte zwischen $0$ und $N/2-1$ annehmen. Für $N = 8$ gilt:
- $$w^0 = 1,\hspace{0.2cm}w^1 = {1}/{\sqrt{2}}- {\rm j} \cdot{1}/{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm j},\hspace{0.2cm}w^3 = -{1}/{\sqrt{2}}- {\rm j} \cdot{1}/{\sqrt{2}} \hspace{0.05cm}.$$
Mit dieser Aufgabe sollen die für die FFT erforderliche Anzahl von Rechenoperationen $(O_{\rm FFT})$ ermittelt und mit dem für die DFT angebbaren Wert $O_{\rm DFT} ≈ 8\cdot N^2$ verglichen werden.
Zu beachten ist:
- Sinnvollerweise werden die Potenzen von $w$ vor dem eigentlichen Algorithmus berechnet und in einer Lookup–Tabelle abgelegt. Die hierfür notwendigen Operationen sollen deshalb unberücksichtigt bleiben.
- Die Bitumkehroperation – eine Umsortierung, die vor der ersten Stufe durchzuführen ist – soll bei dieser Abschätzung ebenfalls nicht berücksichtigt werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fast-Fouriertransformation (FFT).
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
a) Jede komplexe Addition erfordert zwei reelle Additionen:
$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 +
R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}
\hspace{0.15 cm}\underline{ A_{\rm A} =
2}\hspace{0.05cm}.$$
b) Eine jede komplexe Multiplikation benötigt vier reelle Multiplikationen und zwei reelle Additionen:
$$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot
R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot
I_1)$$
$$\Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{A_{\rm M} = 2,\hspace{0.3cm}M_{\rm M} =
4} \hspace{0.05cm}.$$
c) Die Basisoperationen lauten mit den komplexen Eingangsgrößen E1, E2 und wμ:
$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$
$$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$
Dies bedeutet eine komplexe Multiplikation und zwei komplexe Additionen:
$$\hspace{0.15 cm}\underline{a_{\rm B} = 2, \hspace{0.2cm}m_{\rm B} = 1}
\hspace{0.05cm}.$$
d) Im Gegensatz zu den Computern in der Anfangszeit nimmt heute eine Multiplikation keine wesentlich größere Rechenzeit in Anspruch als eine Addition bzw. Subtraktion. Mit den Ergebnissen aus a), b) und c) erhält man für die Gesamtzahl der Rechenoperationen:
$$ O_{\rm B} = a_{\rm B}\cdot A_{\rm A} + a_{\rm B}\cdot (A_{\rm M}
+M_{\rm M} ) = 2 \cdot 2 + 1 \cdot 6\hspace{0.15 cm}\underline{ = 10}
\hspace{0.05cm}.$$
e) Insgesamt gibt es ld N Stufen, in denen jeweils N/2 Basisoperationen auszuführen sind:
$$O_{\rm FFT} = {\rm ld}\hspace{0.1cm}N \cdot \frac{N}{2}\cdot
O_{\rm B} = 5 \cdot N \cdot {\rm ld}\hspace{0.1cm}N$$
$$\Rightarrow \hspace{0.3cm}O_{\rm FFT}\hspace{0.1cm}(N=16) = 5\cdot 16 \cdot
4 \hspace{0.15 cm}\underline{= 320}, $$ $$\hspace{0.3cm}O_{\rm FFT}\hspace{0.1cm}(N=1024) = 5\cdot 1024
\cdot 10 \hspace{0.15 cm}\underline{= 51200}
\hspace{0.05cm}.$$
f) Der Rechenzeitgewinn der FFT gegenüber der herkömmlichen DFT ergibt sich zu:
$$G_{\rm FFT} = \frac{O_{\rm DFT}}{O_{\rm FFT}} = \frac{8 \cdot N^2} {5 \cdot
N \cdot {\rm ld}\hspace{0.1cm}N }= 1.6 \cdot \frac{N}{ {\rm
ld}\hspace{0.1cm}N}$$
$$\Rightarrow \hspace{0.3cm}G_{\rm FFT} \hspace{0.1cm}(N=16) = 1.6 \cdot
\frac{16}{ 4} \hspace{0.15 cm}\underline{= 6.4},$$ $$ \hspace{0.3cm}G_{\rm FFT} \hspace{0.1cm}(N=1024) = 1.6 \cdot\frac{1024}{ 10}\hspace{0.15 cm}\underline{ \approx 164}
\hspace{0.05cm}.$$