Difference between revisions of "Aufgaben:Exercise 4.5Z: Again Mutual Information"
| Line 100: | Line 100: | ||
:* Für die Transinformation gilt stets <i>I</i>(<i>X</i>; <i>Y</i>) ≥ 0. | :* Für die Transinformation gilt stets <i>I</i>(<i>X</i>; <i>Y</i>) ≥ 0. | ||
:* Im wertdiskreten Fall gibt es keine negative Entropie, jedoch im wertkontinuierlichen. | :* Im wertdiskreten Fall gibt es keine negative Entropie, jedoch im wertkontinuierlichen. | ||
| − | + | [[File: P_ID2898__Inf_Z_4_5d.png |center|]] | |
| − | + | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 16:10, 4 April 2017
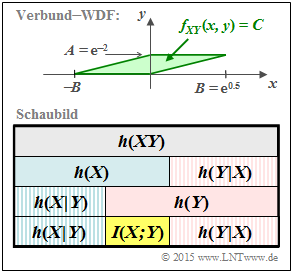
Die Grafik zeigt oben die in dieser Aufgabe zu betrachtende Verbund–WDF fXY(x, y), die identisch ist mit der „grünen” Konstellation in Aufgabe A4.5. Die Skizze ist in der y–Richtung um den Faktor 3 vergrößert. Im grün hinterlegten Definitionsgebiet ist die Verbund–WDF konstant gleich C = 1/F, wobei F die Fläche des Parallelogramms angibt.
In der Aufgabe A4.5 wurden folgende differentielle Entropien berechnet: $$h(X) \ = \ {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A\hspace{0.05cm})\hspace{0.05cm},$$ $$h(Y) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}B \cdot \sqrt{ {\rm e } } \hspace{0.05cm})\hspace{0.05cm},$$ $$h(XY) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}F \hspace{0.05cm}) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A \cdot B \hspace{0.05cm})\hspace{0.05cm}.$$ In dieser Aufgabe sind nun die speziellen Parameterwerte A = e–2 und B = e0.5 zu verwenden. Außerdem ist zu beachten:
- Bei Verwendung des natürlichen Logarithmus „ln” ist die Pseudo–Einheit „nat” anzufügen.
- Verwendet man den Logarithmus dualis ⇒ „log2”, so ergeben sich alle Größen in „bit”.
Entsprechend dem obigen Schaubild sollen nun auch die bedingten differentiellen Entropien h(Y|X) und h(X|Y) ermittelt und deren Bezug zur Transinformation I(X;Y) angegeben werden.
Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.2.
Fragebogen
Musterlösung
- Die Zufallsgröße X ist gleichverteilt zwischen 0 und 1/e2 = e–2:
$$h(X) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-2}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -2\,{\rm nat}}\hspace{0.05cm}. $$
- Die Zufallsgröße Y ist dreieckverteilt zwischen ±e0.5:
$$h(Y) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}\sqrt{ {\rm e} } \cdot \sqrt{ {\rm e} } ) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{ { \rm e } } \hspace{0.05cm}) \hspace{0.15cm}\underline{= +1\,{\rm nat}}\hspace{0.05cm}.$$
- Die Fläche des Parallelogramms ergibt sich zu
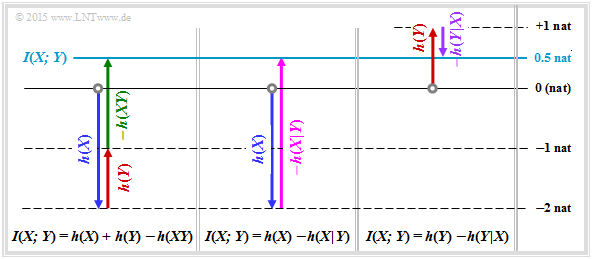
$$F = A \cdot B = {\rm e}^{-2} \cdot {\rm e}^{0.5} = {\rm e}^{-1.5}\hspace{0.05cm}.$$ Damit hat die 2D–WDF im grün hinterlegten Bereich die konstante Höhe C = 1/F = e1.5 und man erhält für die Verbundentropie: $$h(XY) = {\rm ln} \hspace{0.1cm} (F) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-1.5}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -1.5\,{\rm nat}}\hspace{0.05cm}.$$ Daraus ergibt sich für die Transinformation: $$I(X;Y) = h(X) + h(Y) - h(XY) = -2 \,{\rm nat} + 1 \,{\rm nat} - (-1.5 \,{\rm nat} ) \hspace{0.15cm}\underline{= 0.5\,{\rm nat}}\hspace{0.05cm}.$$ b) Allgemein gilt der Zusammenhang log2(x) = ln(x)/ln(2). $$h(X) \ = \ \frac{-2\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.886\,{\rm bit}}\hspace{0.05cm},$$ $$h(Y) \ = \ \frac{+1\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= +1.443\,{\rm bit}}\hspace{0.05cm},$$ $$h(XY) \ = \ \frac{-1.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.164\,{\rm bit}}\hspace{0.05cm},$$ $$I(X;Y) \ = \ \frac{0.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ Oder auch: $$I(X;Y) = -2.886 \,{\rm bit} + 1.443 \,{\rm bit}+ 2.164 \,{\rm bit}{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ c) Die Transinformation kann auch in der Form I(X; Y) = h(Y) – h(Y|X) geschrieben werden: $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 1 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= 0.5\,{\rm nat}= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ d) Für die differentielle Rückschlussentropie gilt entsprechend: $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = -2 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= -2.5\,{\rm nat}= -3.607\,{\rm bit}}\hspace{0.05cm}.$$ Alle hier berechneten Größen sind in der Grafik am Seitenende zusammengestellt. Pfeile nach oben kennzeichnen einen positiven Beitrag, Pfeile nach unten einen negativen.
e) Richtig sind die Lösungsvorschläge 1 bis 3. Nochmals zur Verdeutlichung:
- Für die Transinformation gilt stets I(X; Y) ≥ 0.
- Im wertdiskreten Fall gibt es keine negative Entropie, jedoch im wertkontinuierlichen.