Difference between revisions of "Aufgaben:Exercise 4.7: Several Parallel Gaussian Channels"

Revision as of 14:28, 5 April 2017

Die Kanalkapazität des AWGN–Kanals ⇒ Y = X + N wurde im Theorieteil wie folgt angegeben (mit Zusatz–Einheit „bit”)

$$C_{\rm AWGN}(P_X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right )\hspace{0.05cm}.$$ Die verwendeten Größen haben folgende Bedeutung:

P_X</sb> ist die Sendeleistung ⇒ Varianz der Zufallsgröße X,
P_N</sb> ist die Störleistung ⇒ Varianz der Zufallsgröße N.

Werden K identische Gaußkanäle parallel genutzt, so gilt für die Gesamtkapazität: $$C_K(P_X) = K \cdot C_{\rm AWGN}(P_X/K) \hspace{0.05cm}.$$ Hierbei ist berücksichtigt, dass

in jedem Kanal die gleiche Störleistung P_N vorliegt,
somit jeder Kanal die gleiche Sendeleistung erhält,
die Gesamtleistung genau wie im Fall K = 1 gleich P_X ist.

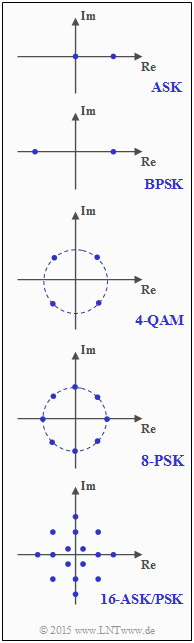
In nebenstehender Grafik sind die Signalraumpunkte für einige digitale Modulationsverfahren angegeben:

Amplitude Shift Keying (ASK)
Binary Phase Shift Keying (BPSK)
Quadratur-Amplitudenmodulation (hier: 4-QAM)
Phase Shift Keying (hier: 8–PSK ⇒ DVB–2)
Kombinierte ASK/PSK-Modulation (hier: 16-ASK/PSK)

Zu Beginn dieser Aufgabe ist zu prüfen, welcher K–Parameter für die einzelnen Verfahren gültig ist.

Hinweis: Die Aufgabe gehört zu Kapitel 4.2.

Fragebogen

$ASK: K$ =

$BPSK: K$ =

$4-QAM: K$ =

$8-PSK: K $ =

$16-ASK/PSK: K $ =

	C_K = K/2 · log₂ [1 + P_X/P_N].
	C_K = K/2 · log₂ [1 + P_X/(K · P_N)].
	C_K = 1/2 · log₂ [1 + P_X/P_N)].

$PX/PN = 15, K = 1: CK$ =

$K = 2: CK$ =

$K = 4: CK$ =

	Ja: Die größte Kanalkapazität ergibt sich für K = 2.
	Ja: Die größte Kanalkapazität ergibt sich für K = 4.
	Nein: Je größer K, desto größer ist die Kanalkapazität.
	Der Grenzwert für K → ∞ (in bit) ist C_K = P_X/P_N/2/ln(2).

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.

@@ Line 31: / Line 31: @@
 <quiz display=simple>
-{Multiple-Choice Frage
+{Welche Parameter <i>K</i> gelten für die folgenden Modulationsverfahren?
+|type="{}"}
+$ASK: K$ = { 1 3% }
+$BPSK: K$ = { 1 3% }
+$4-QAM: K$ = { 2 3% }
+$8-PSK: K $ = { 2 3% }
+$16-ASK/PSK: K $ = { 2 3% }
+{Welche Kanalkapazität <i>C<sub>K</sub></i> ergibt sich für <i>K</i> gleich gute Kanäle (jeweils mit der Störleistung  <i>P<sub>N</sub></i> und der Sendeleistung <i>P<sub>X</sub></i>/<i>K</i>)?
 |type="[]"}
-- Falsch
+- <i>C<sub>K</sub></i> = <i>K</i>/2 &middot; log<sub>2</sub> [1 + <i>P<sub>X</sub></i>/<i>P<sub>N</sub></i>].
-+ Richtig
++ <i>C<sub>K</sub></i> = <i>K</i>/2 &middot; log<sub>2</sub> [1 + <i>P<sub>X</sub></i>/(<i>K</i> &middot; <i>P<sub>N</sub></i>)].
+- <i>C<sub>K</sub></i> = 1/2 &middot; log<sub>2</sub> [1 + <i>P<sub>X</sub></i>/<i>P<sub>N</sub></i>)].
-{Input-Box Frage
+{Welche Kapazitäten ergeben sich für <i>P<sub>X</sub></i>/<i>P<sub>N</sub></i> = 15?
 |type="{}"}
-$\alpha$ = { 0.3 }
+$PX/PN = 15,  K = 1:   CK$ = { 2 3% }
+$K = 2:   CK$ = { 3.087 3% }
+$K = 4:   CK$ = { 4.496 3% }
+{Gibt es bezüglich der Kanalzahl <i>K</i> ein (theoretisches) Optimum?
+|type="[]"}
+- Ja: Die größte Kanalkapazität ergibt sich für <i>K</i> = 2.
+- Ja: Die größte Kanalkapazität ergibt sich für <i>K</i> = 4.
++ Nein: Je größer <i>K</i>, desto größer ist die Kanalkapazität.
+- Der Grenzwert für <i>K</i> &#8594; &#8734; (in bit) ist <i>C<sub>K</sub></i> = <i>P<sub>X</sub></i>/<i>P<sub>N</sub></i>/2/ln(2).