Aufgaben:Exercise 1.5Z: Symmetrical Markov Source

• Return to book

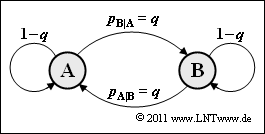
In der Aufgabe 1.5 wurde eine binäre Markovquelle behandelt, bei der die Übergangswahrscheinlichkeiten von $\rm A$ nach $\rm B$ und von $\rm B$ nach $\rm A$ unterschiedlich waren. In dieser Aufgabe soll nun gelten:

$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q \hspace{0.8cm} ( 0 \le q \le 1) \hspace{0.05cm}.$$

Alle in der Aufgabe 1.5 angegebenen Gleichungen gelten auch hier:

• Entropie:

$$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm},$$

• Erste Entropienäherung:

$$H_{\rm 1} = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm B}} \hspace{0.05cm},$$

• k–te Entropienäherung ($k = 2, 3$, ...):

$$H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H] \hspace{0.05cm},\hspace{0.5cm}H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
• Bezug genommen wird insbesondere auf die Seite Binärquellen mit Markoveigenschaften.
• Bei allen Entropien ist die Pseudoeinheit „bit/Symbol” hinzuzufügen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie die Symbolwahrscheinlichkeiten für die Übergangswahrscheinlichkeit $q = 1/4$.

$p_{\rm A} \ = $

$p_{\rm B} \ = $

2

Berechnen Sie die Quellenentropie $H$ für $q = 1/4$.

$H \ =$ $\ \rm bit/Symbol$

3

Welche Entropienäherungen erhält man für $q = 1/4$?

$H_1 \ =$ $\ \rm bit/Symbol$

$H_2 \ =$ $\ \rm bit/Symbol$

$H_3 \ =$ $\ \rm bit/Symbol$

4

Bestimmen Sie $q$ derart, dass H maximal wird. Interpretation.

$H \rightarrow \text{Maximum:}\ \ q \ =$

5

Welche Symbolfolgen sind mit $q = 0$ möglich?

	$\rm AAAAAA$ ...
	$\rm BBBBBB$ ...
	$\rm ABABAB$ ...

6

Welche Symbolfolgen sind mit $q = 0$ möglich?

	$\rm AAAAAA$ ...
	$\rm BBBBBB$ ...
	$\rm ABABAB$ ...

Musterlösung

Solution

(1)  Bei einer stationären binären Markovquelle erster Ordnung gilt:

$$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} + p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-q) \cdot p_{\rm A} + q \cdot p_{\rm B}$$

$$q \cdot p_{\rm A} = q \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm A} = p_{\rm B}\hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm}.$$

(2)  Zur Berechnung der Entropie $H$ benötigt man alle vier Verbundwahrscheinlichkeiten:

$$p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot(1-q) = p_{\rm BB}\hspace{0.05cm},\hspace{1cm} p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot q = p_{\rm BA}\hspace{0.05cm}.$$

Setzt man diese Werte in die gegebene Entropie–Gleichung ein, so erhält man

$$H = 2 \cdot \frac{1}{2} \cdot(1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} + 2 \cdot \frac{1}{2} \cdot q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} = q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} + (1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} = H_{\rm bin}(q) \hspace{0.05cm}.$$

Der gesuchte Zahlenwert ist $H = H_{\rm bin} (0.25) \hspace{0.15cm}\underline{= 0.811 \, \rm bit/Symbol}$.

(3)  Bei gleichwahrscheinlichen Binärsymbolen ist $H_1 \hspace{0.15cm}\underline{= 1 \, \rm bit/Symbol}$. Mit der für Markovquellen gültigen Gleichung gilt weiter:

$$H_2 \hspace{0.1cm} = \hspace{0.1cm} {1}/{2} \cdot [ H_1 + H] \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} \hspace{0.05cm},$$

$$ H_3 \hspace{0.1cm} = \hspace{0.1cm} {1}/{3} \cdot [ H_1 + 2 H] \hspace{0.15cm} \underline {= 0.874 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(4)  Das Maximum der binären Entropiefunktion ergibt sich für $q\hspace{0.15cm}\underline{= 0.5}$. Damit beträgt die maximale Entropie $H = 1 \, \rm bit/Symbol$. Man erkennt aus der Beziehung $H = H_1$ und aus dem vorne abgebildeten Übergangsdiagramm, dass $q = 0.5$ statistisch unabhängige Symbole zur Folge hat:

$$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = 0.5 \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}= 0.5 \hspace{0.05cm}.$$

(5)  Richtig sind die Lösungsvorschläge 1 und 2:

• Die Symbolfolge ergibt sich entweder zu $\rm AAAAAA$ ... oder zu $\rm BBBBBB$ ... , je nachdem, welches Symbol als Startwert vorgegeben wurde.
• Die Entropie einer solchen Quelle ist $H = H_{\rm bin}(0) = 0$.

(6)  Richtig ist nur der Lösungsvorschlag 3:

• Nun kann weder $\rm A$ direkt auf $\rm A$ noch $\rm B$ direkt auf $\rm B$ folgen.
• Es ergibt sich stets eine alternierende Folge, je nach Startwert die Folge $\rm ABABAB$ ... oder $\rm BABABA$... .
• Diese Quelle hat in beiden Fällen die Entropie $H = H_{\rm bin}(1) = 0$.