Difference between revisions of "Aufgaben:Exercise 1.3: System Comparison at AWGN Channel"
m (Guenter verschob die Seite 1.3 Vergleich beim AWGN–Kanal nach 1.3 Systemvergleich beim AWGN–Kanal) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
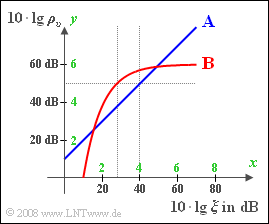
| − | [[File:P_ID960__Mod_A_1_3.png|right|]] | + | [[File:P_ID960__Mod_A_1_3.png|right|frame|Zum Systemvergleich beim AWGN–Kanal]] |
| − | Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten | + | Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten[[Modulationsverfahren/Qualitätskriterien#Einige_Anmerkungen_zum_AWGN.E2.80.93Kanalmodell|AWGN–Kanal]] aus und beschreiben folgendes doppelt–logarithmische Diagramm: |
| − | + | *Die Ordinate gibt den Sinken–Störabstand (SNR logarithmiert) $10 · \lg ρ_v$ in dB an. | |
| − | + | *Auf der Abszisse ist $10 · \lg ξ$ aufgetragen, wobei für die normierte Leistungskenngröße gilt: | |
| − | $$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$ | + | :$$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$ |
| − | + | *In $ξ$ sind also die Sendeleistung $P_{\rm S}$, der Kanaldämpfungsfaktor $α_{\rm K}$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{\rm NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst. | |
| − | + | * Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden: | |
| − | $$ | + | :$$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm |
| + | K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = | ||
| + | 10^{-10}\;{\rm W}/{\rm Hz}\hspace{0.05cm}, \hspace{0.2cm} | ||
| + | B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$ | ||
| + | |||
In der Grafik sind zwei Systeme eingezeichnet, deren (x, y)–Verlauf wie folgt beschrieben werden kann: | In der Grafik sind zwei Systeme eingezeichnet, deren (x, y)–Verlauf wie folgt beschrieben werden kann: | ||
| − | :*'''System | + | *Das '''System A''' ist gekennzeichnet durch die folgende Gleichung: |
| + | :$$y = x+1.$$ | ||
| + | *Entsprechend gilt für das '''System B:''' | ||
| + | :$$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$ | ||
| + | Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung: | ||
| + | :$$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$ | ||
| + | So steht $x = 4$ für $10 · \lg ξ = 40$ dB bzw. $ξ = 10^4$ und $y = 5$ steht für $10 · \lg ρ_v= 50$ dB, also $ρ_v = 10^5$. | ||
| − | |||
| − | |||
| − | + | ''Hinweise:'' | |
| − | Die | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. |
| − | + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Qualitätskriterien#Signal.E2.80.93zu.E2.80.93St.C3.B6r.E2.80.93Leistungsverh.C3.A4ltnis|Signal-zu-Stör-Leistungsverhältnis]] und auf das Kapitel [[Lineare_zeitinvariante_Systeme/Lineare_Verzerrungen|Lineare Verzerrungen]] im Buch „Lineare zeitinvariante Systeme”. | |
| − | + | *Durch die Angabe der Leistungen in $\rm W$ sind diese unabhängig vom Betugswiderstand $R$. | |
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | + | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 16:55, 19 June 2017
Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genanntenAWGN–Kanal aus und beschreiben folgendes doppelt–logarithmische Diagramm:
- Die Ordinate gibt den Sinken–Störabstand (SNR logarithmiert) $10 · \lg ρ_v$ in dB an.
- Auf der Abszisse ist $10 · \lg ξ$ aufgetragen, wobei für die normierte Leistungskenngröße gilt:
- $$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$
- In $ξ$ sind also die Sendeleistung $P_{\rm S}$, der Kanaldämpfungsfaktor $α_{\rm K}$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{\rm NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst.
- Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden:
- $$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = 10^{-10}\;{\rm W}/{\rm Hz}\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$
In der Grafik sind zwei Systeme eingezeichnet, deren (x, y)–Verlauf wie folgt beschrieben werden kann:
- Das System A ist gekennzeichnet durch die folgende Gleichung:
- $$y = x+1.$$
- Entsprechend gilt für das System B:
- $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$
Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung:
- $$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$
So steht $x = 4$ für $10 · \lg ξ = 40$ dB bzw. $ξ = 10^4$ und $y = 5$ steht für $10 · \lg ρ_v= 50$ dB, also $ρ_v = 10^5$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Qualitätskriterien.
- Bezug genommen wird insbesondere auf die Seite Signal-zu-Stör-Leistungsverhältnis und auf das Kapitel Lineare Verzerrungen im Buch „Lineare zeitinvariante Systeme”.
- Durch die Angabe der Leistungen in $\rm W$ sind diese unabhängig vom Betugswiderstand $R$.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Dies entspricht gegenüber dem bisher betrachteten System einer Erhöhung des Störabstandes um 10 dB, so dass auch $10 · lg ξ$ um 10 dB erhöht werden muss.
$$10 \cdot {\rm lg} \hspace{0.1cm}\xi = 50\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \xi=10^5 \hspace{0.05cm}.$$
Ein 10–fach größerer $ξ$–Wert wird erreicht – vorausgesetzt die anderen Parameter bleiben jeweils gleich:
- durch die Sendeleistung $P_S = 50 kW$ statt 5 $kW$,
- durch den Dämpfungsfaktor $α_K = 0.00316$ anstelle von $0.001$,
- durch die Rauschleistungsdichte $N_0 = 10°{ –11 } W/Hz$ statt $10^{ –10 } W/Hz$,
- durch die Bandbreite $B_{NF} = 0.5 kHz$ statt $5 kHz$.
Richtig sind also die Alternativen 2 und 3.
3. Für $10 · lg ξ = 40$ dB ist die Hilfsgröße $x = 4$. Damit ergibt sich für die Hilfsgröße der Ordinate: $$y= 6 \cdot \left(1 - {\rm e}^{-3} \right)\approx 5.7 \hspace{0.05cm}.$$ Dies entspricht dem Sinken–Störabstand $10 · lg ρ_υ = 57$ dB, also einer Verbesserung gegenüber dem System A um 7 dB.
4.Diese Problemstellung wird durch folgende Gleichung beschrieben: $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right) = 5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm e}^{-x+1} ={1}/{6}$$ $$ \Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \approx 2.79 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 27.9\,{\rm dB}\hspace{0.05cm}.$$ Bei System A war hierfür $10 · lg ξ = 40$ dB notwendig, was bei den weiter gegebenen Zahlenwerten durch $P_S = 5$ kW erreicht wurde. Nun kann die Sendeleistung um etwa 12.1 dB verringert werden: $$ 10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}}= -12.1\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}} = 10^{-1.21}\approx 0.06\hspace{0.05cm}.$$ Das bedeutet, dass bei System B mit nur 6% der Sendeleistung von System A – also mit nur 0.3 kW – die gleiche Systemqualität erzielt wird.
5.Wir bezeichnen mit V (steht für Verbesserung) den größeren Sinken–Störabstand von System B gegenüber System A:
$$V = 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;B)} - 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;A)}$$
$$ = \left[6 \cdot \left(1 - {\rm e}^{-x+1} \right) -x -1 \right] \cdot 10\,{\rm dB}\hspace{0.05cm}.$$
Durch Nullsetzen der Ableitung ergibt sich derjenige x–Wert, der zur maximalen Verbesserung führt:
$$ \frac{{\rm d}V}{{\rm d}x} = 6 \cdot {\rm e}^{-x+1} -1\Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = \hspace{0.15cm}\underline {27.9\,{\rm dB}}\hspace{0.05cm}.$$
Es ergibt sich also genau der in (d) behandelte Fall mit $10 · lg ρ_υ = 50$ dB, während der Störabstand bei System A nur 37.9 dB beträgt. Die Verbesserung ist demnach 12.1 dB.