Aufgaben:Exercise 3.2: Spectrum with Angle Modulation

• Return to book

Tabelle der Besselfunktionen

Es wird hier von folgenden Gleichungen ausgegangen:

• Quellensignal:

$$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

• Sendesignal:

$$s(t) = 1\,{\rm V} \cdot \cos(2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t))\hspace{0.05cm},$$

• idealer Kanal, d.h. das Empfangssignal:

$$r(t) = s(t) = 1\,{\rm V} \cdot \cos(2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t))\hspace{0.05cm},$$

• idealer Demodulator;

$$ v(t) = \frac{1}{ K_{\rm M}} \cdot \phi(t)\hspace{0.05cm}.$$

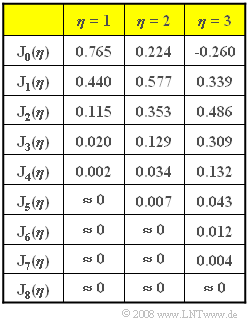
Die Grafik zeigt die Besselfunktionen erster Art und n-ter Ordnung in tabellarischer Form.

Hinweise:

• Die Aufgabe gehört zum Kapitel Phasenmodulation.
• Bezug genommen wird insbesondere auf die Seiten Spektralfunktion eines phasenmodulierten Sinussignals sowie Interpretation des Besselspektrums.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welches Modulationsverfahren liegt hier vor?

	Amplitudenmodulation.
	Phasenmodulation.
	Frequenzmodulation.

2

Welches Modulationsverfahren würden Sie wählen, wenn die Kanalbandbreite nur $B_{\rm K} = 10 \ \rm kHz$ betragen würde?

	Amplitudenmodulation.
	Phasenmodulation.
	Frequenzmodulation.

3

Wie ist die Modulatorkonstante $K_{\rm M}$ zu wählen, damit der Phasenhub $η = 1$ beträgt?

$K_{\rm M} \ = \ $ $\ \rm 1/V$

4

Berechnen Sie das Spektrum $S_{\rm TP}(f)$ des äquivalenten Tiefpass–Signals $s_{\rm TP}(t)$.
Wie groß sind die Gewichte der Spektrallinien bei $f = 0$ und $f = -3 \ \rm kHz$?

$S_{\rm TP}(f = 0)\ = \ $ $\ \rm V$

$S_{\rm TP}(f = -3\ \rm kHz) \ = \ $ $\ \rm V$

5

Berechnen Sie die Spektren des analytischen Signals $s_{\rm +}(t)$sowie des physikalischen Signals $s(t)$.
Wie groß sind die Gewichte der Spektrallinien bei $f = 97 \ \rm kHz$?

$S_+(f = 97 \ \rm kHz)\ = \ $ $\ \rm V$

$S(f = 97 \ \rm kHz)\hspace{0.32cm} = \ $ $\ \rm V$

6

Wie groß ist die erforderliche Kanalbandbreite $B_{\rm K}$ für $ η = 1$, wenn man (betragsmäßige) Impulsgewichte kleiner als $0.01$ vernachlässigt?

$η = 1\text{:} \ \ \ B_{\rm K}\ = \ $ $\ \rm kHz$

7

Welche Kanalbandbreiten würden sich für $η = 2$ und $η = 3$ ergeben?

$η = 2\text{:} \ \ \ B_{\rm K}\ = \ $ $\ \rm kHz$

$η = 3\text{:} \ \ \ B_{\rm K}\ = \ $ $\ \rm kHz$

Musterlösung

Solution

(1)  Die Phase $ϕ(t)$ ist proportional zum Quellensignal $q(t)$   ⇒   es handelt sich um eine Phasenmodulation   ⇒   Antwort 2.

(2)  Eine Winkelmodulation (PM, FM) führt bei bandbegrenztem Kanal stets zu nichtlinearen Verzerrungen. Bei Zweiseitenband-Amplitudenmodulation (ZSB-AM) ist hier dagegen bereits mit $B_{\rm K} = 6 \ \rm kHz$ eine verzerrungsfreie Übertragung möglich   ⇒   Antwort 1.

(3)  Der Modulationsindex (oder Phasenhub) ist bei Phasenmodulation gleich $η = K_{\rm M} · A_{\rm N}$. Somit ist die Modulatorkonstante $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ zu wählen, damit sich $η = 1$ ergibt.

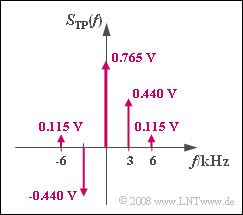
(4)  Es liegt ein sogenanntes Besselspektrum vor:

$$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$

Dieses ist ein diskretes Spektrum mit Anteilen bei $f = n · f_{\rm N}$, wobei $n$ ganzzahlig ist. Die Gewichte der Diracfunktionen sind durch die Besselfunktionen gegeben. Mit $A_{\rm T} = 1\ \rm V$ erhält man:

PM–Spektrum im äquivalenten Tiefpass–Bereich

$$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$

$$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$

$$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$

Aufgrund der Symmetrie ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ erhält man für die Spektrallinie bei $f = -3 \ \rm kHz$:

$$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$

Anmerkung: Eigentlich müsste man für den Spektralwert bei $f = 0$ schreiben:

$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$

Dieser ist somit aufgrund der Diracfunktion unendlich groß, lediglich das Gewicht der Diracfunktion ist endlich. Gleiches gilt für alle diskreten Spektrallinien.

(5)  $S_+(f)$ ergibt sich aus $S_{\rm TP}(f)$ durch Verschiebung um $f_{\rm T}$ nach rechts. Deshalb ist

$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$

Das tatsächliche Spektrum unterscheidet sich von $S_+(f)$ bei positiven Frequenzen um den Faktor $1/2$:

$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$

Allgemein kann geschrieben werden:

$$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$

(6)  Unter der vorgeschlagenen Vernachlässigung können alle Bessellinien ${\rm J}_{|n|>3}$ außer Acht gelassen werden. Damit erhält man $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$.

(7)  Die Zahlenwerte in der Tabelle auf der Angabenseite zeigen, dass nun folgende Kanalbandbreiten erforderlich wären:

• für $η = 2$:     $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$,
• für $η = 3$:     $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$