Aufgaben:Exercise 4.3: Natural and Discrete Sampling

• Return to book

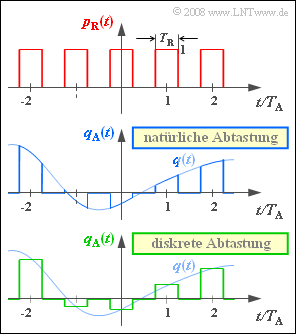
Die ideale Abtastung lässt sich im Zeitbereich durch Multiplikation des analogen Quellensignals $q(t)$ mit einem Diracpuls $p_δ(t)$ beschreiben: $$ q_{\rm A}(t) = p_{\delta}(t) \cdot q(t) \hspace{0.05cm}.$$ Diracimpulse – unendlich schmal und unendlich hoch – und dementsprechend auch der Diracpuls $p_δ(t)$ lassen sich in der Praxis jedoch nicht realisieren. Hier muss statt dessen vom Rechteckpuls $p_R(t)$ ausgegangen werden, wobei folgender Zusammenhang gilt: $$ p_{\rm R}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \right ]\star g_{\rm R}(t)$$ mit $$ g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm}. \\ \end{array}$$ Die Dauer $T_R$ eines Rechteckimpulses sollte dabei (deutlich) kleiner sein als der Abstand $T_A$ zweier Abtastwerte. In der Grafik ist dieses Verhältnis mit $T_R/T_A = 0.5$ sehr groß gewählt, um den Unterschied zwischen der sog. natürlichen und der sog. diskreten Abtastung besonders deutlich werden zu lassen:

• Bei natürlicher Abtastung ist das abgetastete Signal $q_A(t)$ gleich dem Produkt aus Rechteckpuls $p_R(t)$ und analogem Quellensignal $q(t)$:

$$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)\hspace{0.05cm}.$$

• Dagegen lautet die entsprechende Gleichung für die diskrete Abtastung:

$$ q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \cdot q(t)\right ]\star g_{\rm R}(t)\hspace{0.05cm}.$$ In der Grafik sind diese Signale in blau (natürliche Abtastung) bzw. grün (diskrete Abtastung) skizziert.

Zur Signalrekonstruktion wird ein rechteckförmiger Tiefpass $H(f)$ mit der Grenzfrequenz $f_G = f_A/2$ und der Verstärkung $T_A/T_R$ im Durchlassbereich eingesetzt: $$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}. \\ \end{array}$$ Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1 dieses Buches.

Fragebogen

1

Es gelte $T_R/T_A = 0.5$. Geben Sie hierfür das normierte Spektrum $G_R(f)/T_A$ an. Welcher Spektralwert tritt bei $f = 0$ auf?

$G_R(f=0)/T_A$ =

2

Wie lautet das Spektrum $Q_A(f)$ bei natürlicher Abtastung? Vorschläge:

	$Q_A(f) = P_δ(f) ∗ Q(f)$,
	$Q_A(f) = [P_δ(f) · (G_R(f)/TA)] ∗ Q(f)$,
	$Q_A(f) = [P_δ(f) ∗ Q(f)] · (G_R(f)/TA)$.

3

Eignet sich bei natürlicher Abtastung der angegebene Tiefpass zur Interpolation?

	ja
	nein

4

Wie lautet das Spektrum $Q_A(f)$ bei diskreter Abtastung? Vorschläge:

	$Q_A(f) = P_δ(f) ∗ Q(f)$,
	$Q_A(f) = [P-δ(f) · (G_R(f)/T_A)] ∗ Q(f)$,
	$Q_A(f) = [P_δ(f) ∗ Q(f)] · G_R(f)/T_A$.

5

Eignet sich bei diskreter Abtastung der angegebene Tiefpass zur Interpolation?

	ja
	nein

Musterlösung

Solution

1. Das Spektrum des Rechteckimpulses $g_R(t)$ mit Amplitude 1 und Dauer $T_R$ lautet: $$ G_{\rm R}(f) = T_{\rm R} \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.3cm} {\rm mit}\hspace{0.3cm} {\rm si}(x) = \sin(x)/x$$ $$\Rightarrow \hspace{0.3cm} \frac{G_{\rm R}(f)}{T_{\rm A}} = \frac{T_{\rm R}}{T_{\rm A}} \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{G_{\rm R}(f = 0)}{T_{\rm A}} =\frac{T_{\rm R}}{T_{\rm A}}\hspace{0.15cm}\underline { = 0.5} \hspace{0.05cm}.$$

2. Richtig ist der zweite Lösungsvorschlag. Aus der angegebenen Gleichung im Zeitbereich ergibt sich mit dem Faltungssatz: $$q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)$$ $$\Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ \frac{1}{T_{\rm A}}\cdot P_{\rm \delta}(f) \cdot G_{\rm R}(f) \right ] \star Q(f) = \left [ P_{\rm \delta}(f) \cdot \frac{G_{\rm R}(f)}{{T_{\rm A}}} \right ] \star Q(f) \hspace{0.05cm}.$$ Der erste Lösungsvorschlag gilt nur bei idealer Abtastung und der letzte bei diskreter Abtastung.

3. Die Antwort ist JA. Ausgehend von dem Ergebnis aus b) erhält man mit der Spektralfunktion des Diracpulses $$Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \cdot \frac{G_{\rm R}(f)}{{T_{\rm A}}} \right ] \star Q(f)= \left [ \frac{G_{\rm R}(f)}{{T_{\rm A}}} \cdot \sum_{\mu = -\infty}^{+\infty} \delta(f - \mu \cdot f_{\rm A})\right ] \star Q(f) \hspace{0.05cm}.$$ Ist das Abtasttheorem erfüllt und der Tiefpass richtig dimensioniert, so liegen von den unendlich vielen Faltungsprodukten nur das Faltungsprodukt mit $μ = 0$ im Durchlassbereich. Unter Berücksichtigung des Verstärkungsfaktors $T_A/T_R$ erhält man somit für das Spektrum am Filterausgang: $$V(f) = \frac{T_{\rm A}}{T_{\rm R}} \cdot \left [ \frac{G_{\rm R}(f = 0)}{{T_{\rm A}}} \cdot \delta(f )\right ] \star Q(f)= Q(f) \hspace{0.05cm}.$$ 4. Richtig ist der letzte Lösungsvorschlag. Verlagert man den Faktor $1/T_A$ zum Rechteckimpuls, so erhält man bei diskreter Abtastung mit dem Faltungssatz: $$ q_{\rm A}(t) = \left [ p_{\rm \delta}(t)\cdot q(t) \right ] \star \frac{g_{\rm R}(t)}{T_{\rm A}}$$ $$\Rightarrow \hspace{0.3cm}Q_{\rm A}(f)= \left [ P_{\rm \delta}(f)\star Q(f) \right ] \cdot \frac{G_{\rm R}(f)}{T_{\rm A}}\hspace{0.05cm}.$$

5. Die Antwort ist NEIN. Die Gewichtungsfunktion $G_R(f)$ betrifft nun auch den inneren Kern ($μ = 0$) des Faltungsproduktes. Alle anderen Terme ($μ ≠ 0$) werden durch den Tiefpass eliminiert. Man erhält hier im relevanten Bereich $|f| < f_A/2$: $$V(f) = \frac{T_{\rm A}}{T_{\rm R}} \cdot \frac{G_{\rm R}(f )}{{T_{\rm A}}} \cdot Q(f) = 2 \cdot 0.5 \cdot {\rm si}(\pi f T_{\rm R})\cdot Q(f)$$ $$ \Rightarrow \hspace{0.3cm}V(f) = Q(f) \cdot {\rm si}(\pi f T_{\rm R})\hspace{0.05cm}.$$ Sieht man hier keine zusätzliche Entzerrung vor, so werden die höheren Frequenzen entsprechend der si–Funktion gedämpft. Die höchste Signalfrequenz ($f = f_A/2$) wird hierbei am stärksten abgesenkt: $$V(f = \frac{f_{\rm A}}{2}) = Q( \frac{f_{\rm A}}{2}) \cdot {\rm si}(\pi \cdot \frac{T_{\rm R}}{2 \cdot T_{\rm A}})=$$ $$ = Q( \frac{f_{\rm A}}{2}) \cdot {\rm si}(\pi \cdot \frac{\sin(\pi/4)}{\pi/4})\approx 0.9 \cdot Q( \frac{f_{\rm A}}{2}) \hspace{0.05cm}.$$