Aufgaben:Exercise 5.3: PACF of PN Sequences

• Return to book

M–Sequenz mit P = 15 und zyklische Vertauschungen

Mit einem rückgekoppelten Schieberegister vom Grad $G$ lässt sich eine Spreizfolge $〈c_ν〉$ mit der (maximalen) Periodenlänge $P = 2^G - 1$ erzeugen, wenn die Rückführungskoeffizienten (Anzapfungen) richtig gewählt sind.

In dieser Aufgabe wird der in der linken Grafik von Beispiel 1 im Theorieteil dargestelle PN–Generator mit der Oktalkennung (31) betrachtet, der wegen $G = 4$ eine Folge mit der Periodenlänge $P = 15$ liefert.

In der Grafik sind die unipolare Folge $〈u_ν〉$ mit $u_ν ∈ \{0, 1\}$ und daraus abgeleitete zyklische Verschiebungen $〈u_{ν+λ}〉$ dargestellt, wobei der Verschiebungsparameter $λ$ Werte zwischen $1$ und $15$ annimmt. Eine Verschiebung um $λ$ bedeutet dabei absolut einen Versatz um $λ · T_c$. Hierbei bezeichnet $T_c$ die Chipdauer.

Für den Einsatz in einem CDMA–System verwendet man allerdings die bipolare (antipodische) Folge $〈c_ν〉$ mit $c_ν ∈ \{+1, -1\}$, die ab der Teilaufgabe (5) untersucht werden soll. Gesucht ist deren periodische Autokorrelationsfunktion (PAKF)

$${\it \varphi}_{c}(\lambda) = {\rm E} \left [ c_\nu \cdot c_{\nu+\lambda} \right ] \hspace{0.05cm}.$$

Zur Herleitung soll zunächst die PAKF

$${\it \varphi}_{u}(\lambda) = {\rm E}\left [ u_\nu \cdot u_{\nu+\lambda} \right ]$$

mit den unipolaren Koeffizienten $u_ν ∈ \{0, 1\}$ berechnet werden. Die Umrechnung der Koeffizienten ist durch $c_ν = 1 – 2u_ν$ gegeben.

Hinweise:

• Die Aufgabe gehört zum Kapitel Spreizfolgen für CDMA.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie groß ist der Grad des PN–Generators?

$G$ =

2

Wie groß ist der quadratische Erwartungswert der Koeffizienten $u_ν$ ∈ {0, 1}?

$E[u_ν^2]$ =

3

Wie groß ist der quadratische Erwartungswert der Koeffizienten $c_ν$ ∈ {+1, –1}?

$E[u_c^2]$ =

4

Welche Aussagen gelten für den Erwartungswert $E[u_ν · u_{ν+λ}]$?

	Es ist $E[u_ν · u_{ν+1}] = 4/15$.
	Es ist $E[u_ν · u_{ν+2}] = 4/15$.
	Die PAKF–Werte $φ_u(λ = 1)$, ... , $φ_u(λ = 14)$ sind alle gleich.

5

Berechnen Sie die PAKF–Werte bei bipolarer Darstellung ($λ = 1, ..., 14$):

$φ_c(λ)$ =

6

Geben Sie folgende PAKF–Werte für den Fall G = 6 an.

$φ_c(λ=0)$ =

$φ_c(λ=0)$ =

$φ_c(λ=63)$ =

$φ_c(λ=64)$ =

Musterlösung

Solution

1. Die Periodendauer einer M–Sequenz beträgt $$P = 2^G -1 \hspace{0.05cm}.$$ Daraus ergibt sich mit P = 15 der Grad G = 4.

2. Von den P = 15 Spreizbits sind 8 Einsen und 7 Nullen. Damit gilt wegen $u_ν^2 = u_ν$: $${\rm E}\left [ u_\nu \right ] = {\rm E}\left [ u_\nu^2 \right ] = \frac{8}{15} \hspace{0.15cm}\underline {\approx 0.533} \hspace{0.05cm}, \hspace{0.3cm} {\rm allgemein:}\,\, \frac{P+1}{2P}\hspace{0.05cm}.$$

3. In bipolarer Darstellung ist $c_ν^2$ immer 1. Damit gilt auch für den quadratischen Erwartungswert: $${\rm E}\left [ c_\nu^2 \right ] \hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$

4. Die beigefügte Tabelle macht deutlich, dass für die diskreten PAKF–Werte mit λ = 1, ... , 14 gilt: $${\it \varphi}_{u}(\lambda) = {\rm E}\left [ u_\nu \cdot u_{\nu+\lambda} \right ]= \frac{4}{15} \hspace{0.05cm}.$$ Multipliziert man nämlich 〈$u_ν$〉 mit 〈$u_{ν+λ}$〉, wobei für den Index λ wieder die Werte 1, ... , 14 einzusetzen sind, so treten im Produkt jeweils 4 Einsen auf. Dagegen gilt für λ = P = 15: $${\it \varphi}_{u}(\lambda = 15) = {\rm E}\left [ u_\nu \cdot u_{\nu+P} \right ]= \frac{8}{15} \hspace{0.05cm}.$$ Richtig sind somit die Lösungsvorschläge 1, 2 und 4.

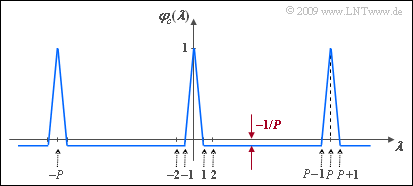
5. Die bipolaren Koeffizienten $c_ν$ ergeben sich aus den unipolaren Koeffizienten uν gemäß der Gleichung $$c_\nu = 1 - 2 \cdot u_\nu \hspace{0.3cm} \Rightarrow \hspace{0.3cm} u_\nu = 0: c_\nu = +1\hspace{0.05cm},\hspace{0.3cm}u_\nu = 1: c_\nu = -1 \hspace{0.05cm}.$$ Damit folgt aus den Rechenregeln für Erwartungswerte: $${\it \varphi}_{c}(\lambda) = {\rm E} \left [ c_\nu \cdot c_{\nu+\lambda} \right ]= {\rm E} \left [ (1 - 2 \cdot u_\nu ) \cdot (1 - 2 \cdot u_\nu ) \right ] =$$ $$ = 1 + 4 \cdot {\rm E}\left [ u_\nu \cdot u_{\nu+\lambda} \right ] - 2 \cdot {\rm E}\left [ u_\nu \right ] - 2 \cdot {\rm E}\left [ u_{\nu+\lambda} \right ] \hspace{0.05cm}.$$ Mit dem Ergebnis der Teilaufgabe b) $$ {\rm E}\left [ u_{\nu} \right ]= {\rm E}\left [ u_{\nu+\lambda} \right ]=\frac{8}{15} \hspace{0.05cm},$$ und der Teilaufgabe d) $${\rm E}\left [ u_\nu \cdot u_{\nu+\lambda} \right ] =\frac{4}{15} \hspace{0.05cm} \,\,{\rm{f\ddot{u}r}}\,\,\lambda = 0, \pm P, \pm 2P, ...$$ kommt man somit zum Ergebnis (falls λ kein Vielfaches von P): $${\it \varphi}_{c}(\lambda) = 1 + 4 \cdot \frac{4}{15} - 2 \cdot \frac{8}{15}- 2 \cdot \frac{8}{15} \hspace{0.15cm}\underline {\approx - 0.067} = - \frac{1}{15} = - \frac{1}{P} \hspace{0.05cm}.$$

6. Eine M–Sequenz mit Grad G = 6 hat die Periodenlänge P = 63. Entsprechend dem Ergebnis zur Teilaufgabe e) erhält man somit: $$ {\it \varphi}_{c}(\lambda = 0) = {\it \varphi}_{c}(\lambda =63) \hspace{0.15cm}\underline {= 1} \hspace{0.05cm},\hspace{0.3cm} {\it \varphi}_{c}(\lambda = 1) = {\it \varphi}_{c}(\lambda =64) \hspace{0.15cm}\underline {= -1/63} \hspace{0.05cm}.$$ Die nachfolgende Grafik zeigt die PAKF einer M–Sequenz allgemein. Für die hier gesuchten Ergebnisse ist P = 63 zu setzen.