Aufgaben:Exercise 4.14Z: Offset QPSK vs. MSK

• Return to book

Koeffizientenzuordnung bei O-QPSK und MSK

Eine Realisierungsmöglichkeit für die MSK bietet die Offset–QPSK (kurz: O–QPSK), wie aus den Blockschaltbildern im Theorieteil hervorgeht.

Beim normalen Offset–QPSK–Betrieb werden jeweils zwei Bit der Quellensymbolfolge $〈q_k〉$ einem Bit $a_{{\rm I}ν}$ im Inphasezweig und sowie einem Bit $a_{{\rm Q}ν}$ im Quadraturzweig zugeordnet.

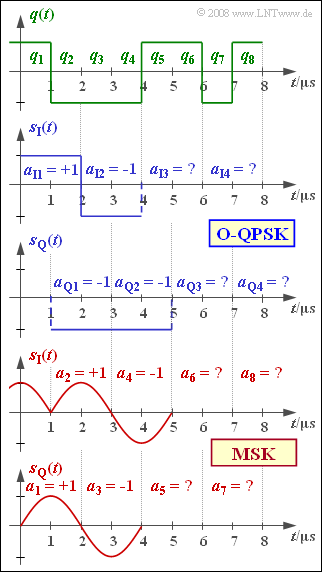
Die Grafik zeigt diese Seriell–Parallel–Wandlung in den drei oberen Diagrammen für die ersten vier Bit des grün gezeichneten Quellensignals $q(t)$. Dabei ist zu beachten:

• Die Darstellung der Offset–QPSK gilt für einen rechteckigförmigen Grundimpuls. Die Koeffizienten $a_{{\rm I}ν}$ und $a_{{\rm Q}ν}$ können die Werte $±1$ annehmen.
• Durchläuft der Zeitindex der Quellensymbole die Werte $k =1,$ ... $, 8$, so nimmt die Zeitvariable $ν$ nur die Werte $1,$ ... $, 4$ an.
• Die Skizze berücksichtigt auch den Zeitversatz (Offset) für den Quadraturzweig.

Bei der MSK–Realisierung mittels Offset–QPSK ist eine Umcodierung erforderlich. Hierbei gilt mit $q_k ∈ \{+1, –1\}$ und $a_k ∈ \{+1, –1\}$:

$$a_k = (-1)^{k+1} \cdot a_{k-1} \cdot q_k \hspace{0.05cm}.$$

Beispielsweise erhält man unter der Annahme $a_0 = +1$:

$$a_1 = a_0 \cdot q_1 = +1,\hspace{0.2cm}a_2 = -a_1 \cdot q_2 = +1,$$

$$a_3 = a_2 \cdot q_3 = -1,\hspace{0.2cm}a_4 = -a_3 \cdot q_4 = -1 \hspace{0.05cm}.$$

Weiter ist zu berücksichtigen:

• Die Koeffizienten $a_0 = +1$, $a_2 = +1$, $a_4 = -1$ sowie die noch zu berechnenden Koeffizienten $a_6$ und $a_8$ werden dem Signal $s_{\rm I}(t)$ zugeordnet.
• Dagegen werden die Koeffizienten $a_1 = +1$ und $a_3 = -1$ sowie alle weiteren Koeffizienten mit ungeradem Index dem Signal $s_{\rm Q}(t)$ beaufschlagt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Nichtlineare digitale Modulation.
• Bezug genommen wird insbesondere auf den Abschnitt Realisierung der MSK als Offset-QPSK.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• In Aufgabe 4.14 wird die zugehörige Phasenfunktion $ϕ(t)$ ermittelt, wobei ebenfalls der (normierte) MSK–Grundimpuls zugrunde liegt:

$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos (\frac{\pi \cdot t}{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f:\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}. \\ \end{array}$$

Fragebogen

1

Wie groß ist die Bitdauer $T_{\rm B}$ des Quellensignals?

$T_{\rm B} \ = \ $ $\ \rm μs$

2

Wie groß ist die Symboldauer $T$ der Offset–QPSK?

$T \ = \ $ $\ \rm μs$

3

Geben Sie die genannten Amplitudenkoeffizienten der Offset–QPSK an.

$a_{\rm I3} \hspace{0.25cm} = \ $

$a_{\rm Q3} \ = \ $

$a_{\rm I4} \hspace{0.25cm} = \ $

$a_{\rm Q4} \ = \ $

4

Wie groß ist die Symboldauer $T$ der MSK?

$T \ = \ $ $\ \rm μs$

5

Geben Sie die genannten Amplitudenkoeffizienten der MSK an.

$a_5 \ = \ $

$a_6 \ = \ $

$a_7 \ = \ $

$a_8 \ = \ $

Musterlösung

Solution

(1)  Aus der oberen Skizze kann man $T_{\rm B} \hspace{0.15cm}\underline{ = 1 \ \rm μs}$ ablesen.

(2)  Bei QPSK bzw. Offset–QPSK ist aufgrund der Seriell–Parallel–Wandlung die Symboldauer $T$ doppelt so groß wie die Bitdauer $T_{\rm B}$:

$$ T = 2 \cdot T_{\rm B} \hspace{0.15cm}\underline {= 2\,{\rm \mu s}} \hspace{0.05cm}.$$

(3)  Entsprechend der aus der Skizze für die ersten Bit erkennbaren Zuordnung gilt:

$$ a_{\rm I3} = q_5 \hspace{0.15cm}\underline {= +1},$$

$$a_{\rm Q3} = q_6 \hspace{0.15cm}\underline {= +1},$$

$$a_{\rm I4} = q_7 \hspace{0.15cm}\underline { = -1},$$

$$a_{\rm Q4} = q_8 \hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$

(4)  Bei der MSK ist die Symboldauer $T$ gleich der Bitdauer $T_{\rm B}$:

$$T = T_{\rm B}\hspace{0.15cm}\underline { = 1\,{\rm \mu s}} \hspace{0.05cm}.$$

(5)  Entsprechend der angegebenen Umcodiervorschrift gilt mit $a_4 = –1$:

$$q_5 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_5 = a_4 \cdot q_5 \hspace{0.15cm}\underline {= -1},$$

$$q_6 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_6 = -a_5 \cdot q_6 \hspace{0.15cm}\underline {= +1},$$

$$ q_7 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_7 = a_6 \cdot q_7 \hspace{0.15cm}\underline {= -1}, $$

$$q_8 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}a_8 = -a_7 \cdot q_8\hspace{0.15cm}\underline { = +1}\hspace{0.05cm}.$$