Difference between revisions of "Aufgaben:Exercise 5.8Z: Cyclic Prefix and Guard Interval"
| Line 7: | Line 7: | ||
*Die Übertragung erfolgt über einen Zweiwegekanal, wobei beide Pfade verzögert sind. Die Kanalimpulsantwort lautet somit mit $τ_1 = \ \rm 50 μs$ und $τ_2 = 125\ \rm μs$: | *Die Übertragung erfolgt über einen Zweiwegekanal, wobei beide Pfade verzögert sind. Die Kanalimpulsantwort lautet somit mit $τ_1 = \ \rm 50 μs$ und $τ_2 = 125\ \rm μs$: | ||
:$$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$ | :$$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$ | ||
| − | Der Einsatz eines solchen zyklischen Präfixes vermindert allerdings die Bandbreiteneffizienz (Verhältnis von Symbolrate zu Bandbreite) um den Faktor | + | *Der Einsatz eines solchen zyklischen Präfixes vermindert allerdings die Bandbreiteneffizienz (Verhältnis von Symbolrate zu Bandbreite) um den Faktor |
:$$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$ | :$$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$ | ||
| − | und führt auch zu einer Verringerung des Signal–Rausch–Verhältnisses um ebenfalls diesen Wert <i>β</i>. | + | :und führt auch zu einer Verringerung des Signal–Rausch–Verhältnisses um ebenfalls diesen Wert <i>β</i>. |
*Voraussetzung für die Gültigkeit des hier angegebenen SNR–Verlustes ist allerdings, dass die Impulsantworten $g_{\rm S}(t)$ und $g_{\rm E}(t)$ von Sende– und Empfangsfilter an die Symboldauer $T$ angepasst sind (Matched–Filter–Ansatz). | *Voraussetzung für die Gültigkeit des hier angegebenen SNR–Verlustes ist allerdings, dass die Impulsantworten $g_{\rm S}(t)$ und $g_{\rm E}(t)$ von Sende– und Empfangsfilter an die Symboldauer $T$ angepasst sind (Matched–Filter–Ansatz). | ||
| Line 15: | Line 15: | ||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Realisierung_von_OFDM-Systemen|Realisierung von OFDM-Systemen]]. | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Realisierung_von_OFDM-Systemen|Realisierung von OFDM-Systemen]]. | ||
| − | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Realisierung_von_OFDM-Systemen#Zyklisches_Pr.C3.A4fix|Zyklisches Präfix]]sowie [[Modulationsverfahren/Realisierung_von_OFDM-Systemen#OFDM.E2.80.93System_mit_zyklischem_Pr.C3.A4fix|OFDM-System | + | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Realisierung_von_OFDM-Systemen#Zyklisches_Pr.C3.A4fix|Zyklisches Präfix]] sowie [[Modulationsverfahren/Realisierung_von_OFDM-Systemen#OFDM.E2.80.93System_mit_zyklischem_Pr.C3.A4fix|OFDM-System mit zyklischem Präfix]]. |
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 23: | Line 23: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie die Kernsymboldauer an. | + | {Geben Sie die Kernsymboldauer $T$ an. |
|type="{}"} | |type="{}"} | ||
| − | $T$ | + | $T \ = \ $ { 250 3% } $\ \rm μs$ |
| − | {Wie lang sollte das Guard–Intervall mindestens sein? | + | {Wie lang sollte das Guard–Intervall $T_{\rm G}$ mindestens sein? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $T_{\rm G}\ = \ $ { 125 3% } $\ \rm μs$ |
| − | {Bestimmen Sie die resultierende Rahmendauer. | + | {Bestimmen Sie die resultierende Rahmendauer $T_{\rm R}$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $T_{\rm R}\ = \ $ { 375 3% } $\ \rm μs$ |
{Welche Aussagen sind richtig? Durch eine Guardlücke, also das Nullsetzen des OFDM–Signals im Guard–Intervall, können | {Welche Aussagen sind richtig? Durch eine Guardlücke, also das Nullsetzen des OFDM–Signals im Guard–Intervall, können | ||
| Line 45: | Line 45: | ||
+ Impulsinterferenzen (ISI) unterdrückt werden. | + Impulsinterferenzen (ISI) unterdrückt werden. | ||
| − | {Nennen Sie die jeweilige Anzahl der Abtastwerte für | + | {Nennen Sie die jeweilige Anzahl der Abtastwerte für das Kernsymbol $(N)$, das Guard–Intervall $(N_{\rm G})$ und den gesamten Rahmen $(N_{\rm R})$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $N \ = \ $ { 8 } |
| − | $\ | + | $N_{\rm G} \ = \ $ { 4 } |
| − | + | $N_{\rm R} \ = \ $ { 12 } | |
| − | {Geben Sie unter der Vorraussetzung, dass lediglich der erste Träger mit dem Trägerkoeffizienten | + | {Geben Sie unter der Vorraussetzung, dass lediglich der erste Träger mit dem Trägerkoeffizienten $-1$ verwendet wird, die Abtastwerte des Guard–Intervalls vor der Übertragung über den Kanal an. |
|type="{}"} | |type="{}"} | ||
| − | $\text{Re | + | $\text{Re}[d_{-1}] \ = \ $ { -714--0.700 } |
| − | $\text{Im | + | $\text{Im}[d_{-1}] \ = \ $ { 0.707 1% } |
| − | $\text{Re | + | $\text{Re}[d_{-2}] \ = \ $ { 0. } |
| − | $\text{Im | + | $\text{Im}[d_{-2}] \ = \ $ { 1 1% } |
| − | $\text{Re | + | $\text{Re}[d_{-3}] \ = \ $ { 1 1% } |
| − | $\text{Im | + | $\text{Im}[d_{-3}] \ = \ $ { -714--0.700 } |
| − | $\text{Re | + | $\text{Re}[d_{-4}] \ = \ $ { 1 1% } |
| − | $\text{Im | + | $\text{Im}[d_{-4}] \ = \ $ { 0. } |
| − | {Welche Bandbreiteneffizienz ergibt sich inklusive des Guard–Intervalls? | + | {Welche Bandbreiteneffizienz $\beta$ ergibt sich inklusive des Guard–Intervalls? |
|type="{}"} | |type="{}"} | ||
| − | $\beta$ | + | $\beta\ = \ $ { 0.667 3% } |
| − | {Wie groß ist der damit verbundene SNR–Verlust unter der Voraussetzung des Matched–Filter–Ansatzes? | + | {Wie groß ist der damit verbundene SNR–Verlust $10 · \lg \ Δ_ρ$ (in dB) unter der Voraussetzung des Matched–Filter–Ansatzes? |
|type="{}"} | |type="{}"} | ||
| − | $10 · lg Δ_ρ$ | + | $10 · \lg \ Δ_ρ \ = \ $ { 1.76 3% } $\ \rm dB$ |
</quiz> | </quiz> | ||
Revision as of 11:51, 8 August 2017
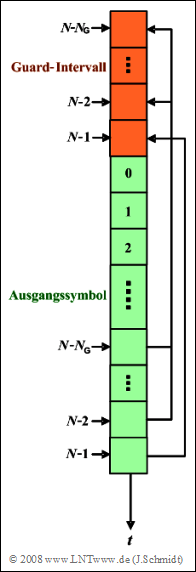
Wir gehen in dieser Aufgabe von einem OFDM–System mit $N = 8$ Trägern und zyklischem Präfix aus. Der Subträgerabstand sei $f_0 = 4 \ \rm kHz$. Die Grafik zeigt das Prinzip des zyklischen Präfixes.
- Die Übertragung erfolgt über einen Zweiwegekanal, wobei beide Pfade verzögert sind. Die Kanalimpulsantwort lautet somit mit $τ_1 = \ \rm 50 μs$ und $τ_2 = 125\ \rm μs$:
- $$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$
- Der Einsatz eines solchen zyklischen Präfixes vermindert allerdings die Bandbreiteneffizienz (Verhältnis von Symbolrate zu Bandbreite) um den Faktor
- $$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$
- und führt auch zu einer Verringerung des Signal–Rausch–Verhältnisses um ebenfalls diesen Wert β.
- Voraussetzung für die Gültigkeit des hier angegebenen SNR–Verlustes ist allerdings, dass die Impulsantworten $g_{\rm S}(t)$ und $g_{\rm E}(t)$ von Sende– und Empfangsfilter an die Symboldauer $T$ angepasst sind (Matched–Filter–Ansatz).
Hinweise:
- Die Aufgabe gehört zum Kapitel Realisierung von OFDM-Systemen.
- Bezug genommen wird insbesondere auf die Seiten Zyklisches Präfix sowie OFDM-System mit zyklischem Präfix.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Um Interferenzen zu vermeiden, ist die Dauer des Guard–Intervalls mindestens so groß zu wählen wie die maximale Verzögerung (hier: $τ_2 = 125 μs$) des Kanals ⇒ $T_G = 125 μs$.
3. Für die Rahmendauer gilt somit: $$ T_{\rm{R}} = T + T_{\rm{G}}\hspace{0.15cm}\underline {= 375\,\,{\rm \mu s}}.$$
4. Durch eine Guardlücke geeigneter Länge können ausschließlich Impulsinterferenzen (ISI) vermieden werden. Die Lückendauer $T_G$ muss dabei so groß gewählt werden, dass das aktuelle Symbol durch das Vorgängersymbol nicht beeinträchtigt wird. Im vorliegenden Beispiel muss $T_G ≥ 125 μs$ sein. Richtig ist der Lösungsvorschlag 2.
5. Durch ein zyklisches Präfix geeigneter Länge werden zusätzlich auch Intercarrier–Interferenzen (ICI) unterdrückt. Es wird damit sichergestellt, dass für alle Träger innerhalb der Kernsymboldauer T eine vollständige und unverfälschte Schwingung auftritt, auch wenn andere Träger aktiv sind. Das heißt: Beide Lösungsvorschläge sind zutreffend.
6. Die Anzahl der Abtastwerte innerhalb des Kernsymbols ist gleich der Anzahl N = 8 der Träger. Wegen $T_G = T/2$ gilt $N_G = 4$ und damit $N_{gesamt} = 12$.
7. Die Belegung des ersten Trägers (Frequenz $f_0$) mit dem Koeffizienten –1 führt zu den Abtastwerten
d0 = –1, d1 = –0.707 – j · 0.707, d2 = –j, d3 = + 0.707 – j · 0.707,
d4 = + 1, d5 = +0.707 + j · 0.707, d6 = j, d7 = –0.707 + j · 0.707.
Die zyklische Erweiterung liefert die zusätzlichen Abtastwerte d–1 = d7, d–2 = d6, d–3 = d5 und d–4 = d4:
$$\underline{{\rm Re}\{d_{-1}\} = -0.707,\hspace{0.3cm}{\rm Im}\{d_{-1}\} = +0.707,\hspace{0.3cm}{\rm Re}\{d_{-2}\} = 0,\hspace{0.3cm} {\rm Im}\{d_{-2}\} = 1},$$ $$\underline{{\rm Re}\{d_{-3}\} = +0.707,\hspace{0.3cm}{\rm Im}\{d_{-3}\} = +0.707,\hspace{0.3cm}{\rm Re}\{d_{-4}\} = 1,\hspace{0.3cm} {\rm Im}\{d_{-4}\} = 0}.$$
8. Entsprechend der angegebenen Gleichung ist die Bandbreiteneffizienz gleich $$\beta = \frac{1}{1 + {T_{\rm{G}}}/{T}} = \frac{1}{1 + ({125\,\,{\rm \mu s}})/({250\,\,{\rm \mu s}})} \hspace{0.15cm}\underline {= 0.667}.$$ 9. Die Bandbreiteneffizienz β = 2/3 führt zu einem SNR–Verlust von $$10 \cdot {\rm{lg}}\hspace{0.04cm}\Delta \rho = 10 \cdot {\rm{lg}}\hspace{0.04cm}(\beta) \hspace{0.15cm}\underline {\approx1.76\,\,{\rm{dB}}}.$$