Difference between revisions of "Signal Representation/Fourier Series"
| Line 87: | Line 87: | ||
Die Bestimmungsgleichung für den Cosinuskoeffizienten $A_1$ lautet (Integration von 0 bis $T_0$): | Die Bestimmungsgleichung für den Cosinuskoeffizienten $A_1$ lautet (Integration von 0 bis $T_0$): | ||
| − | $$A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}0.4\cdot\cos(\omega_0 t)\,{\rm d}t \; & + &\;\frac{2}{T_0}\cdot \int^{T_0}_{0}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t \\ \; & - &\; \frac{2}{T_0}\cdot \int^{T_0}_{0}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.$$ | + | $$ \begin{align} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}0.4\cdot\cos(\omega_0 t)\,{\rm d}t \; & + &\;\frac{2}{T_0}\cdot \int^{T_0}_{0}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t \\ \; & - &\; \frac{2}{T_0}\cdot \int^{T_0}_{0}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align} $$ |
Das letzte Integral ist aufgrund der Orthogonalität gleich 0; das erste ist ebenfalls 0. Nur der mittlere Term liefert hier einen Beitrag zu $A_1$ = 2 · 0.6 · 0.5 = 0.6. Bei allen weiteren ($n \ge 2$) Cosinuskoeffizienten liefern alle drei Integrale den Wert 0, und es gilt somit stets $A_{n \neq 1}=0$. | Das letzte Integral ist aufgrund der Orthogonalität gleich 0; das erste ist ebenfalls 0. Nur der mittlere Term liefert hier einen Beitrag zu $A_1$ = 2 · 0.6 · 0.5 = 0.6. Bei allen weiteren ($n \ge 2$) Cosinuskoeffizienten liefern alle drei Integrale den Wert 0, und es gilt somit stets $A_{n \neq 1}=0$. | ||
Revision as of 21:02, 25 March 2016
Contents
Allgemeine Beschreibung
Jede periodische Funktion $x(t)$ kann in allen Bereichen, in denen sie stetig ist oder nur endlich viele Sprungstellen aufweist, in eine trigonometrische Reihe entwickelt werden, die man als Fourierreihe bezeichnet.
Die Fourierreihe eines periodischen Signals $x(t)$ lautet wie folgt:
$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$
Hierbei bezeichnen:
- $A_0$ den Gleichanteil von $x(t)$,
- $A_n$ die Cosinuskoeffizienten ,
- $B_n$ die Sinuskoeffizienten,
- $\omega_0 = 2\pi/T_0$ die Grundkreisfrequenz des periodischen Signals ($T_0$ ist die Periodendauer).
Soll die Fourierreihe mit dem tatsächlichen periodischen Signal $x(t)$ exakt übereinstimmen, so müssen im Allgemeinen unendlich viele Cosinus– und Sinuskoeffizienten zur Berechnung herangezogen werden. Bricht man die Fourierreihe ab und verwendet jeweils nur $N$ dieser Koeffizienten An und Bn, so ergibt sich bis auf Sonderfälle ein etwas anderer Funktionsverlauf:
$$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$
Zwischen dem periodischen Signal und der Fourierreihenapproximation gilt der Zusammenhang:
$$x(t)=\lim_{N\to \infty} x_{N}(t).$$
Ist $N \cdot f_0$ die höchste im Signal $x(t)$ vorkommende Frequenz, so gilt natürlich $x_N(t) = x(t)$.
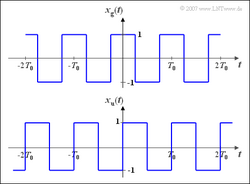
Wir betrachten zwei periodische Rechtecksignale, jeweils mit der Periodendauer $T_0$ und der Grundkreisfrequenz $\omega_0 = 2\pi/T_0$. Für das oben skizzierte gerade Zeitsignal gilt $x_g(-t) = x_g(t)$. Dagegen ist die unten dargestellte Funktion ungerade: $x_u(-t) = -x_u(t)$.
In Formelsammlungen, z. B. [BS01], findet man die Fourierreihendarstellungen beider Signale:
$$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \ldots + \ldots \right ],$$
$$x_{\rm u}(t)=\frac{4}{\pi}\left [ \sin(\omega_0 t)+\frac{1}{3}\cdot\sin(3 \omega_0 t)+\frac{1}{5}\cdot\sin(5 \omega_0 t)+ \ldots + \ldots \right ].$$
Wegen der allgemeingültigen Beziehung
$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, {+} \ldots=\frac{\pi}{4}$$
ergeben sich die Amplituden der beiden Rechtecksignale (Maximalwerte zum Beispiel bei $t$ = 0 bzw. $T_0/4$) jeweils zu 1. Dies lässt sich auch anhand der Signalverläufe in der obigen Grafik verifizieren.
Berechnung der Fourierkoeffizienten
Der Fourierkoeffizient $A_0$ gibt den Gleichanteil an, der durch Mittelung über den Signalverlauf $x(t)$ bestimmt werden kann. Aufgrund der Periodizität genügt die Mittelung über eine Periode:
$$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$
Der Integrationsbereich kann auch von 0 bis $T_0$ (oder über eine anders festgelegte gleich lange Periode) gewählt werden. Die Bestimmung der Fourierkoeffizienten $A_n$ und $B_n$ $(n \ge 1)$ beruht auf der Eigenschaft, dass die harmonischen Cosinusfunktionen und Sinusfunktionen so genannte Orthogonalfunktionen sind. Für diese gilt\[\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad falls \it \quad m=n,\atop \rm sonst} \right.\]
$$\int ^{+T_0/2}_{-T_0/2}\sin(n\omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad falls \it \quad m=n,\atop \rm sonst} \right.$$
$$\int ^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=0 \quad \rm f\ddot{u}r\quad alle \quad \it m, n.$$
Berücksichtigt man diese Gleichungen, so ergeben sich für die Cosinus– und Sinuskoeffizienten:
$$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$
$$B_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\sin(n \omega_0 t)\,{\rm d}t.$$
Nachfolgend finden Sie ein Lernvideo zur weiteren Verdeutlichung dieser Gleichungen: Zur Berechnung der Fourierkoeffizienten (Dauer 3:50)
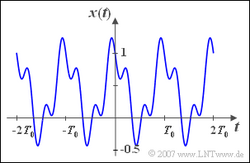
Wir betrachten die nachfolgend gezeichnete periodische Zeitfunktion
$$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$
Da das Integral der Cosinus– und der Sinusfunktion über jeweils eine Periode identisch 0 ist, erhält man für den Gleichsignalkoeffizienten $A_0$ = 0.4.
Die Bestimmungsgleichung für den Cosinuskoeffizienten $A_1$ lautet (Integration von 0 bis $T_0$):
$$ \begin{align} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}0.4\cdot\cos(\omega_0 t)\,{\rm d}t \; & + &\;\frac{2}{T_0}\cdot \int^{T_0}_{0}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t \\ \; & - &\; \frac{2}{T_0}\cdot \int^{T_0}_{0}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align} $$
Das letzte Integral ist aufgrund der Orthogonalität gleich 0; das erste ist ebenfalls 0. Nur der mittlere Term liefert hier einen Beitrag zu $A_1$ = 2 · 0.6 · 0.5 = 0.6. Bei allen weiteren ($n \ge 2$) Cosinuskoeffizienten liefern alle drei Integrale den Wert 0, und es gilt somit stets $A_{n \neq 1}=0$. Die Bestimmungsgleichungen für die Sinuskoeffizienten $B_n$ lauten entsprechend:
$$B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t \; & + & \linebreak \;\frac{2}{T_0} \cdot \int^{T_0}_{0}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t \; \\ \\ & - & \; \frac{2}{T_0}\cdot \int^{T_0}_{0}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t.$$
Für $n \neq 3$ sind alle drei Integralwerte gleich 0 und damit gilt auch $B_n$ = 0. Dagegen liefert für $n=3$ das letzte Integral einen Beitrag, und man erhält für den Sinuskoeffizienten $B_3$ = –0.3.
Ausnutzung von Symmetrieeigenschaften
Einige Erkenntnisse über die zu erwartenden Fourierkoeffizienten $A_n$ und $B_n$ lassen sich bereits aus den Symmetrieeigenschaften der Zeitfunktion $x(t)$ ablesen.
- Ist das Zeitsignal $x(t)$ eine gerade Funktion ⇒ achsensymmetrisch um die Ordinate ($t$ = 0), so verschwinden alle Sinuskoeffizienten $B_n$, da die Sinusfunktion selbst eine ungerade Funktion ⇒ $sin(-\alpha) = -sin(\alpha)$ ist:
$$B_n = 0 \hspace{0.4cm}(n = 1, 2, 3, ...).$$
- Eine ungerade Funktion $x(t)$ ist punktsymmetrisch um den Koordinatenursprung ($t$= 0; $x$ =0). Deshalb müssen hier alle Cosinuskoeffizienten verschwinden ($A_n$ = 0), da die Cosinusfunktion selbst gerade ist. In diesem Fall ist auch der Gleichanteil $A_0$ stets 0.
$$A_n = 0 \hspace{0.4cm}(n = 0, 1, 2, 3, ...).$$
- Liegt eine Funktion ohne Gleichanteil vor ($A_0$ = 0) und ist diese innerhalb einer Periode ungerade ⇒ es gilt $x(t) = -x(t - T_0/2)$, so sind in der Fourierreihendarstellung nur ungerade Vielfache der Grundfrequenz vorhanden. Für die Koeffizienten mit geradzahligem Index gilt dagegen stets:
$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, 4, 6, ...).$$
- Sind alle Koeffizienten $A_n$ und $B_n$ mit geradzahligem Index ($n$ = 2, 4, ...) gleich 0 und der Koeffizient $A_0 \neq 0$, so bezieht sich die im letzten Punkt genannte Symmetrieeigenschaft auf den Gleichsignalanteil, und es gilt:
$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$
Anmerkung: Es können auch mehrere dieser Symmetrieeigenschaften gleichzeitig erfüllt sein. Die Symmetrieeigenschaften der Fourierkoeffizienten werden im ersten Teil des nachfolgenden Videos zusammenfassend dargestellt: Eigenschaften und Genauigkeit der Fourierreihe (Dauer Teil 1: 3:31 – Teil 2: 8:39)
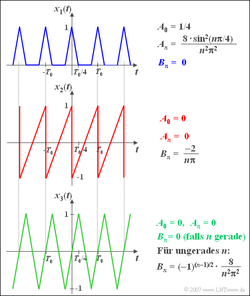
Die oben genannten Eigenschaften werden nun an drei Signalverläufen verdeutlicht. $x_1(t)$ ist eine gerade und mittelwertbehaftete Funktion, die dementsprechend ausschließlich durch Cosinuskoeffizienten $A_n$ bestimmt ist ($B_n$ = 0).
Dagegen sind bei der ungeraden Funktion $x_2(t)$ alle $A_n$ ($n \ge 0$) identisch 0. Die ungerade Funktion $x_3(t)$ beinhaltet ebenfalls nur Sinuskoeffizienten, aber wegen$x_3(t) = -x_3(t - T_0/2)$ ausschließlich für ungeradzahlige Werte von $n$.
Komplexe Fourierreihe
Wie auf der Seite Darstellung mit Cosinus- und Sinusanteil im Kapitel 2.3 für den Fall einer harmonischen Schwingung bereits gezeigt wurde, kann man jedes beliebige periodische Signal
$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$
auch mit Hilfe der Betrags- und Phasenkoeffizienten darstellen:
$$x(t) =C_0+\sum^{\infty}_{n=1}C_{\it n} \cdot\cos(n \omega_0 t-\varphi_n).$$
Diese modifizierten Fourierkoeffizienten weisen folgende Eigenschaften auf:
- Der Gleichsignalkoeffizient $C_0$ ist identisch mit $A_0$.
- Die Betragskoeffizienten lauten: $C_n = (A_n^2 + B_n^2)^{1/2})$.
- Für die Phasenkoeffizienten gilt: $\phi_n$ = arctan ($B_n/A_n$).
Mit der Eulerschen Beziehung cos(x) + j \cdot sin(x) = \text{e}^{jx} erhält man eine zweite Darstellungsvariante der Fourierreihenentwicklung, die von der komplexen Exponentialfunktion ausgeht.
Die komplexe Fourierreihe eines periodischen Signals x(t) lautet wie folgt:
$$x(t)=\sum^{+\infty}_{{\it n}=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}.$$
Hier bezeichnen $D_n$ die komplexen Fourierkoeffizienten, die sich aus den Cosinuskoeffizienten $A_n$ und den Sinuskoeffizienten $B_n$ oder auch aus den Betragskoeffizienten $C_n$ sowie den Phasenkoeffizienten $\phi_n$ wie folgt berechnen lassen (gültig für $n \neq 0$):
$$D_{\it n} =1/2\cdot (A_{\it n}-{\rm j}\cdot B_{\it n})=1/2\cdot C_{\it n}\cdot {\rm e}^{-\rm j \it \varphi_{\it n}} .$$
Die komplexen Fourierkoeffizienten kann man nach folgender Gleichung auch direkt berechnen:
$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \it n\omega_{\rm 0} t}\, {\rm d}t.$$
Solange das Integrationsintervall $T_0$ erhalten bleibt, kann dieses ebenso wie bei den Koeffizienten $A_n$ und $B_n$ beliebig verschoben werden, zum Beispiel von 0 bis $T_0$. Der Koeffizient $D_0$ = $A_0$ ist stets reell. Für die komplexen Koeffizienten mit negativem Laufindex ($n < 0$) gilt:
$$D_{-n}=D_n^\star =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$
Spektrum eines periodischen Signals
Ausgehend von der gerade abgeleiteten komplexen Fourierreihe
$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$
und dem bereits in Kapitel 2.3 benutzten Verschiebungssatz erhält man für das Spektrum eines periodischen Signals $x(t)$:
$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
Dies bedeutet:
- Das Spektrum eines mit T0 periodischen Signals ist ein Linienspektrum bei ganzzahligen Vielfachen der Grundfrequenz $f_0 = 1/T_0$.
- Der Gleichanteil liefert eine Diracfunktion bei $f=0$ mit dem Impulsgewicht $A_0$.
- Daneben gibt es Diracfunktionen $\delta(f \pm n \cdot f_0)$ bei Vielfachen von $f_0$, wobei $\delta(f - n \cdot f_0)$ eine Diracfunktion bei $f= n \cdot f_0$ (also im positiven Frequenzbereich) und $\delta(f - n \cdot f_0)$ eine solche bei der Frequenz $f= -n \cdot f_0$ (im negativen Frequenzbereich) kennzeichnet.
- Die Impulsgewichte sind im allgemeinen komplex.
Diese Aussagen werden auf der nächsten Seite anhand zweier Beispiele verdeutlicht.
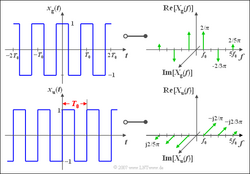
Wir betrachten – wie im Beispiel zu Beginn dieses Abschnitts - zwei periodische Rechtecksignale, jeweils mit Periodendauer $T_0$ und Grundfrequenz $f_0=1/T_0$. Das Signal
$$x_{\rm g}(t)=\frac{4}{\pi} \cdot \left[\cos(\omega_0 t)-\frac{1}{3} \cdot \cos(3\omega_0 t)+\frac{1}{5}\cdot \cos(5\omega_0 t)-\, \ldots + \ldots\right]$$
ist eine gerade, aus verschiedenen Cosinusanteilen zusammengesetzte Funktion. Die zugehörige Spektralfunktion $X_g(f)$ ist damit rein reell. Wie auf der Seite Spektraldarstellung eines Cosinussignals bereits beschrieben wurde, liefert die Grundwelle zwei Diracfunktionen bei $\pm f_0$, jeweils gewichtet mit $2/\pi$. Dieses Gewicht entspricht den (im Allgemeinen komplexen) Fourierkoeffizienten $D_1 = D_-1^\ast$, die nur im Sonderfall einer geraden Funktion reell sind. Weitere Diracfunktionen gibt es bei $\pm 3f_0$ (negativ), $\pm 5f_0$ (positiv), $\pm 7f_0$ (negativ) usw. Alle Phasenwerte $\phi_n$ sind aufgrund der alternierenden Vorzeichen entweder 0 oder $\pi$.
Die unten dargestellte Funktion $x_u(t)$ ist ungerade:
$$x_{\rm u}(t)=\frac{4}{\pi} \cdot \left[\sin(\omega_0 t)+\frac{1}{3} \cdot \sin(3\omega_0 t)+\frac{1}{5} \cdot \sin(5\omega_0 t)+ \ldots\right].$$
Wie auf der Seite Spektraldarstellung eines Sinussignals bereits beschrieben wurde, liefert hier die Grundwelle zwei Diracfunktionen bei $+f_0$ (gewichtet mit $-\text{j}\cdot 2/\pi'"`UNIQ-MathJax29-QINU`"'). Auch alle weiteren Diracfunktionen bei $\pm 3f_0$, $\pm 5f_0$, usw. sind rein imaginär und in gleicher Richtung gewichtet wie die Diracfunktionen bei $\pm f_0$. Die beiden Betragsspektren sind gleich: $|X_u(f)| = |X_g(f)|$. <div style="clear:both;"> </div> </div> =='"`UNIQ--h-5--QINU`"'Das Gibbsche Phänomen== Nicht jedes Signal eignet sich für die Fourierreihendarstellung. Hier einige Einschränkungen: *Eine wichtige Voraussetzung für die Konvergenz der Fourierreihe ist, dass das Signal nur endlich viele Unstetigkeitsstellen je Periode besitzen darf. *An denjenigen Stellen $t=t_i$, an denen $x(t)$ Sprünge aufweist, konvergiert die Reihe gegen den aus dem jeweiligen links– und rechtsseitigen Grenzwert gebildeten arithmetischen Mittelwert. *In der Umgebung solcher Sprungstellen kommt es in der Reihendarstellung meist zu hochfrequenten Oszillationen. Dieser Fehler ist von prinzipieller Art, das heißt, er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Man spricht vom ''Gibbschen Phänomen'', benannt nach dem Physiker Josiah Willard Gibbs. *Durch eine Erhöhung von $N$ wird zwar der fehlerhafte Bereich kleiner, nicht jedoch die maximale Abweichung zwischen dem Signal $x(t)$ und der Fourierreihendarstellung $x_N(t)$. Der maximale Fehler beträgt ca. 9% der Sprungamplitude – und zwar unabhängig von $N$. Das Gibbsche Phänomen und weitere interessante Aspekte werden in einem Lernvideo behandelt: Eigenschaften und Genauigkeit der Fourierreihe (Dauer Teil 1: 3:31 – Teil 2: 8:39) <div class="example"> Links sehen Sie gepunktet einen Ausschnitt eines periodischen $\pm 1$–Rechtecksignals und die dazugehörige Fourierreihendarstellung mit $N$ = 1, 3 und 5 Summanden. Die Grundwelle hat hier den Amplitudenwert $/\pi \approx 1.27$. Auch mit $N$ = 5 (das bedeutet wegen $A_2$ = $A_4$ = 0 drei Summanden) unterscheidet sich die Fourierreihe vom anzunähernden Rechtecksignal noch deutlich, vor allem im Bereich der Flanke. [[File:P_ID2720__Sig_T_2_4_S7_neu.png|250px|right|Zum Gibbschen Phänomen]] Aus dem rechten Bild ist zu erkennen, dass die Flanke und der innere Bereich mit $N$ = 100 relativ gut nachgebildet werden, es aber an der Sprungstelle aufgrund des Gibbschen Phänomens noch immer zu Überschwingern kommt. Da hier die Sprungamplituden jeweils gleich 2 sind, ergeben sich die Maximalwerte näherungsweise zu 1.18. Mit $N$ = 1000 wären die Überschwinger genau so groß, aber auf einen noch engeren Raum begrenzt und bei zeitdiskreter Darstellung eventuell nicht mehr sichtbar.