Difference between revisions of "Aufgaben:Exercise 1.2Z: Bit Error Measurement"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Fehlerwahrscheinlichkeit bei Basisbandübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=…“) |
|||
| Line 4: | Line 4: | ||
| − | [[File:|right|]] | + | [[File:P_ID1265__Dig_Z_1_2.png|right|]] |
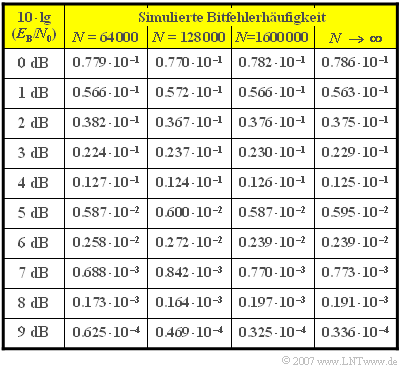
| + | Die Bitfehlerwahrscheinlichkeit $$p_{\rm B} = {1}/{2} \cdot{\rm erfc} \left( \sqrt{\frac{E_{\rm B}}{N_0}}\right)$$ eines Binärsystems wurde durch eine Messung der Bitfehlerquote (BER) $$h_{\rm B} = \frac {n_{\rm B}}{N}$$ simulativ ermittelt. Oftmals wird <i>h</i><sub>B</sub> auch Bitfehlerhäufigkeit genannt. <br><br>In obigen Gleichungen bedeuten | ||
| + | *<i>E</i><sub>B</sub> : Energie pro Bit, | ||
| + | *<i>N</i><sub>0</sub> : AWGN–Rauschleistungsdichte, | ||
| + | *<i>n</i><sub>B</sub> : Anzahl der aufgetretenen Bitfehler, | ||
| + | *<i>N</i> : Anzahl der simulierten Bit einer Versuchsreihe. | ||
| + | |||
| + | Die Tabelle zeigt die Ergebnisse einiger Versuchsreihen mit <i>N</i> = 64000, <i>N</i> = 128000 und <i>N</i> = 1.6 Millionen. Die letzte mit <i>N</i> → ∞ benannte Spalte gibt die Bitfehlerwahrscheinlichkeit <i>p</i><sub>B</sub> wieder. | ||
| + | |||
| + | Im Fragebogen zur Aufgabe wird auf folgende Eigenschaften Bezug genommen: | ||
| + | *Die Bitfehlerhäufigkeit <i>h</i><sub>B</sub> ist in erster Näherung eine gaußverteilte Zufallsgröße mit dem Mittelwert <i>m<sub>h</sub></i> = <i>p</i><sub>B</sub> und der Varianz <i>σ<sub>h</sub></i><sup>2</sup> ≈ <i>p</i><sub>B</sub>/<i>N</i>. | ||
| + | *Die relative Abweichung der Bitfehlerhäufigkeit von der Wahrscheinlichkeit beträgt | ||
| + | |||
| + | $$\varepsilon_{\rm rel}= \frac {h_{\rm B}-p_{\rm B}}{p_{\rm B}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Als eine grobe Faustregel zur erforderlichen Genauigkeit gilt, dass die Anzahl <i>n</i><sub>B</sub> der gemessenen Bitfehler mindestens 100 sein sollte. | ||
| + | <b>Hinweis:</b> Die Aufgabe bezieht sich auf den Lehrstoff von | ||
| + | |||
Revision as of 20:52, 23 October 2017
Die Bitfehlerwahrscheinlichkeit $$p_{\rm B} = {1}/{2} \cdot{\rm erfc} \left( \sqrt{\frac{E_{\rm B}}{N_0}}\right)$$ eines Binärsystems wurde durch eine Messung der Bitfehlerquote (BER) $$h_{\rm B} = \frac {n_{\rm B}}{N}$$ simulativ ermittelt. Oftmals wird hB auch Bitfehlerhäufigkeit genannt.
In obigen Gleichungen bedeuten
- EB : Energie pro Bit,
- N0 : AWGN–Rauschleistungsdichte,
- nB : Anzahl der aufgetretenen Bitfehler,
- N : Anzahl der simulierten Bit einer Versuchsreihe.
Die Tabelle zeigt die Ergebnisse einiger Versuchsreihen mit N = 64000, N = 128000 und N = 1.6 Millionen. Die letzte mit N → ∞ benannte Spalte gibt die Bitfehlerwahrscheinlichkeit pB wieder.
Im Fragebogen zur Aufgabe wird auf folgende Eigenschaften Bezug genommen:
- Die Bitfehlerhäufigkeit hB ist in erster Näherung eine gaußverteilte Zufallsgröße mit dem Mittelwert mh = pB und der Varianz σh2 ≈ pB/N.
- Die relative Abweichung der Bitfehlerhäufigkeit von der Wahrscheinlichkeit beträgt
$$\varepsilon_{\rm rel}= \frac {h_{\rm B}-p_{\rm B}}{p_{\rm B}}\hspace{0.05cm}.$$
- Als eine grobe Faustregel zur erforderlichen Genauigkeit gilt, dass die Anzahl nB der gemessenen Bitfehler mindestens 100 sein sollte.
Hinweis: Die Aufgabe bezieht sich auf den Lehrstoff von
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)