Aufgaben:Exercise 3.3Z: Optimization of a Coaxial Cable System

• Return to book

Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen:

• Die Sendeimpulse sind NRZ–rechteckförmig und besitzen die Energie $E_B = s_0^2 \cdot T$.
• Der Kanal ist ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 40 \, {\rm dB}$.
• Es liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0 = 0.0001 \cdot E_B$ vor.
• Der Empfängerfrequenzgang $H_E(f)$ beinhaltet einen idealen Kanalentzerrer $H_K^{\rm -1}(f)$ und einen Gaußtiefpass $H_G(f)$ mit Grenzfrequenz $f_G$ zur Rauschleistungsbegrenzung.

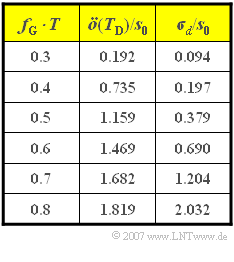
Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_D)$ sowie den Detektionsrauscheffektivwert $\sigma_d$ – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_G$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit

$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}}\right)$$

möglichst klein ist. Die ungünstigste Fehlerwahrscheinlichkeit stellt eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_S$ dar. Für $f_G \cdot T ≥ 0.4$ kann auch eine untere Schranke angegeben werden:

$${1}/{4} \cdot p_{\rm U}\le p_{\rm S}\le p_{\rm U} \hspace{0.05cm}.$$

Hinweis: Die Aufgabe gehört zum Themengebit von Kapitel 3.3. Zur numerischen Auswertung der Q–Funktion können Sie das folgende Interaktionsmodul nutzen: Gaußsche Fehlerfunktion

Fragebogen

1

Bestimmen Sie innerhalb des vorgegebenen Rasters die optimale Grenzfrequenz hinsichtlich des Kriteriums "ungünstigste Fehlerwahrscheinlichkeit".

$f_{\rm G, opt} \cdot T$ =

2

Welche Werte ergeben sich damit für den ungünstigsten Störabstand und die ungünstigste Fehlerwahrscheinlichkeit?

$f_{\rm G, opt}: 10 \cdot {\rm lg} \, \rho_U$ = ${\rm dB}$

$f_{\rm G, opt}: p_U$ = $10^{\rm -2}$

3

Wie müsste man die Rauschleistungsdichte $N_0$ (bezogen auf die Signalenergie) verringern, damit $p_U$ nicht größer ist als $10^{\rm -6}?

$N_0/E_B$ = $10^{\rm -5}$

4

Geben Sie für den unter c) getroffenen Annahmen eine untere und eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_S$ an.

$p_{\rm S, min}$ = $10^{\rm -6}$

$p_{\rm S, max}$ = $10^{\rm -6}$

Musterlösung

Solution

(1) (2) (3) (4) (5)