Aufgaben:Exercise 3.5: Eye Opening with Pseudoternary Coding

• Return to book

Betrachtet werden drei Nachrichtenübertragungssysteme, jeweils mit folgenden übereinstimmenden Eigenschaften:

• NRZ–Rechteckimpulse mit der Amplitude $s_0 = 2 \, {\rm V}$,
• Koaxialkabel mit charakteristischer Kabeldämpfung $a_* = 40 \, {\rm dB}$,
• AWGN–Rauschen mit der Rauschleistungsdichte $N_0$,
• Empfangsfilter, bestehend aus einem idealen Kanalentzerrer und einem Gaußtiefpass mit der normierten Grenzfrequenz $f_G \cdot T \approx 0.5$.
• Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt $T_D = 0$.

Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes:

System A verwendet ein binäres bipolares redundanzfreies Sendesignal. Von diesem System sind folgende Beschreibungsgrößen bekannt:

• Grundimpulswerte $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, ... \, \approx 0$

$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} -g_{1}-g_{-1} = 1.12\,{\rm V} \hspace{0.05cm}.$$

• Rauscheffektivwert $\sigma_d \approx = 0.2 \, {\rm V}$

$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$

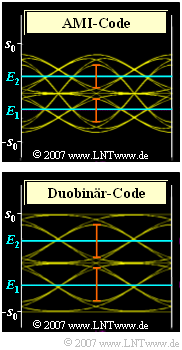
System B verwendet AMI–Codierung. Hier treten die äußeren Symbole $"+1"$ bzw, $"–1"$ nur isoliert auf. Bei drei aufeinanderfolgenden Symbolen sind unter Anderem die zwei Folgen $" \, ... \, , \, +1, \, +1, \, +1, \, ... \,"$ und $" \, ... \, , \, +1, \, 0, \, +1, \, ..."$ nicht möglich im Gegensatz zu $" \, ... \, , \, +1, \, –1, \, +1, \, ... \,"$

System C verwendet Duobinärcode. Hier wird die alternierende Folge $" \, ... \, , \, –1, \, +1, \, –1, \, ... \,"$ durch den Code ausgeschlossen, was sich günstig auf die Augenöffnung auswirkt.

Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 3.4. Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich.

Fragebogen

1

Berechnen Sie die halbe Augenöffnung für den AMI–Code.

${\rm System \, B}: \, \ddot{o}(T_D)/2$ = ${\rm V}$

2

Berechnen Sie den ungünstigsten Störabstand dieses Systems.

${\rm System \, B}: \, 10 \cdot {\rm lg} \, \rho_U$ = ${\rm dB}$

3

Wie müssen die Schwellenwerte $E_1$ und $E_2$ gewählt werden, damit das soeben berechnete Ergebnis stimmt?

$E_1$ = ${\rm V}$

$E_2$ = ${\rm V}$

4

Berechnen Sie die halbe Augenöffnung beim Duobinär–Code.

${\rm System \, C}: \, \ddot{o}(T_D)/2$ = ${\rm V}$

5

Berechnen Sie den ungünstigsten Störabstand bei Duobinärcodierung.

${\rm System \, C}: \, 10 \cdot {\rm lg} \, \rho_U$ = ${\rm dB}$

Musterlösung

Solution

(1) Da beim AMI–Code die Symbolrate gegenüber dem redundanzfreien Binärsystem nicht verändert wird, bleiben die Grundimpulswerte $g_0 = 1.56 \, {\rm V}, g_1 = g_{\rm –1} = 0.22 \, {\rm V}$ und $g_2 = g_{\rm &ndashM2} \approx 0$ unverändert.

Bei Pseudoternärcodierung gibt es stets zwei Augenöffnungen. Die obere Begrenzungslinie des oberen Auges ergibt sich beim AMI–Code wie beim redundanzfreien Binärsystem:

$$d_{\rm oben}= g_0 - 2 \cdot g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm Folge:}-1, +1, -1{\rm )} \hspace{0.05cm}.$$

Dagegen gilt für die untere Begrenzungslinie des oberen Auges:

$$d_{\rm unten}= g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm Folge:}\hspace{0.2cm}0, \hspace{0.05cm}0, +1\hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}+1, \hspace{0.05cm}0, \hspace{0.05cm}0{\rm )}\hspace{0.05cm}.$$

Für die halbe Augenöffnung gilt somit:

$${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm oben} - d_{\rm unten}) = {1}/{2} \cdot g_0 - {3}/{2} \cdot g_1 \hspace{0.15cm}\underline {= 0.45\,{\rm V}}\hspace{0.05cm}.$$

Die entsprechende Gleichung für das redundanzfreie Binärsystem lautet:

$${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$

(2) Bezüglich des Rauschens gibt es keinen Unterschied zwischen den Systemen A, B und C, da stets die gleiche Symbolrate vorliegt. Daraus folgt für den AMI–Code:

$$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$

Die Einbuße gegenüber dem redundanzfreien Binärsystem beträgt somit fast $8 \, {\rm dB}$. Der Grund für diesen gravierenden Störabstandverlust ist, dass beim AMI&ndashMCode trotz $37 %$ Redundanz die bezüglich der Impulsinterferenzen besonders ungünstige Symbolfolge $" \, ... \, , \, –1, \, +1, \, –1, \, ... \,"$ nicht ausgeschlossen wird.

(3) Die Schwelle $E_2 muss in der Mitte zwischen $d_{\rm oben}$ und $d_{\rm unten}$ liegen: :'"`UNIQ-MathJax22-QINU`"' Der Schwellenwert $E_1$ liegt symmetrisch dazu: $E_1 \, \underline {= \, –0.67 {\rm V}}$. '''(4)''' Wir gehen wieder von den gleichen Grundimpulswerten aus. Die ungünstigste Folge bezüglich der oberen Begrenzungslinie des oberen Auges ist $" \, ... \, , \, 0, \, +1, \, 0, \, ... \, "$, während die untere Begrenzungslinie durch $" \, ... \, , \, 0, \, 0, \, +1, \, ... \, "$ bzw. $" \, ... \, , \, +1, \, 0, \, 0, \, ... \, "$ bestimmt wird. Daraus folgt: :'"`UNIQ-MathJax23-QINU`"' '''(5)''' Mit dem Ergebnis aus 4) erhält man analog zur Teilaufgabe 2) :'"`UNIQ-MathJax24-QINU`"' Voraussetzung für dieses Ergebnis sind Schwellenwerte bei :'"`UNIQ-MathJax25-QINU`"' Anzumerken ist, dass hier stets von der gleichen Grenzfrequenz $f_G \cdot T = 0.5$ ausgegangen wurde. Bei Optimierung der Grenzfrequenz kann es durchaus sein, dass der Duobinärcode dem redundanzfreien Binärcode überlegen ist, wenn die charakteristische Kabeldämpfung hinreichend groß ist.