Aufgaben:Exercise 1.2Z: Bit Error Measurement

• Return to book

Simulierte Bitfehlerhäufigkeiten

Die Bitfehlerwahrscheinlichkeit

$$p_{\rm B} = {1}/{2} \cdot{\rm erfc} \left( \sqrt{{E_{\rm B}}/{N_0}}\right)$$

eines Binärsystems wurde durch eine Messung der Bitfehlerquote (BER)

$$h_{\rm B} = {n_{\rm B}}/{N}$$

simulativ ermittelt. Oftmals wird $h_{\rm B}$ auch Bitfehlerhäufigkeit genannt.

In obigen Gleichungen bedeuten:

• $E_{\rm B}$:   die Energie pro Bit,
• $N_0$:   AWGN–Rauschleistungsdichte,
• $n_{\rm B}$:   Anzahl der aufgetretenen Bitfehler,
• $N$:   Anzahl der simulierten Bit einer Versuchsreihe.

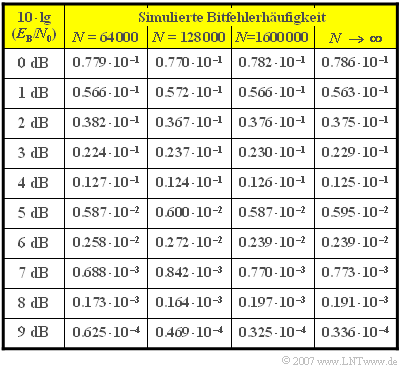
Die Tabelle zeigt die Ergebnisse einiger Versuchsreihen mit $N = 6.4 \cdot 10^4 $, $N = 1. 28 \cdot 10^5$ und $N = 1.6 \cdot 10^6$. Die letzte mit $N \to \infty $ benannte Spalte gibt die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ an.

Im Fragebogen zur Aufgabe wird auf folgende Eigenschaften Bezug genommen:

• Die Bitfehlerhäufigkeit $h_{\rm B}$ ist in erster Näherung eine gaußverteilte Zufallsgröße mit dem Mittelwert $m_h = p_{\rm B}$ und der Varianz $\sigma_h^2 \approx p_{\rm B}$.
• Die relative Abweichung der Bitfehlerhäufigkeit von der Wahrscheinlichkeit beträgt

$$\varepsilon_{\rm rel}= \frac {h_{\rm B}-p_{\rm B}}{p_{\rm B}}\hspace{0.05cm}.$$

• Als eine grobe Faustregel zur erforderlichen Genauigkeit gilt, dass die Anzahl der gemessenen Bitfehler $n_{\rm B} \ge 100$sein sollte.

Hinweise:

• Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Die Genauigkeit der BER–Messung ist unabhängig von $N$.
	Je größer $N$ ist, desto genauer ist im Mittel die BER–Messung.
	Je größer $N$ ist, desto genauer ist jede einzelne BER–Messung.

2

Geben Sie die Streuung $\sigma_h$ für verschiedene $N$ an. Es gelte $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$.

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -3 }\ $

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -3 }\ $

3

Wie groß ist die jeweilige relative Abweichung für $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$?

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \% $

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \% $

4

Geben Sie die Streuung $\sigma_h$ für verschiedene $N$ an. Es gelte $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$.

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -5 }\ $

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -5 }\ $

5

Wie groß ist die jeweilige relative Abweichung für $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$?

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \% $

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \% $

6

Bis zu welchem (logarithmischen) $E_{\rm B}/N_0$–Wert ist $N = 1.6 \cdot 10^6$ aufgrund der Bedingung $n_{\rm B} \ge 100$ ausreichend?

$\text{Maximum} \ [10 \cdot \lg \ E_{\rm B}/N_0] \ = \ $ $\ \rm dB $

Musterlösung

Solution

(1)  Richtig ist nur der zweite Lösungsvorschlag:

• Natürlich wird die Genauigkeit der BER–Messung durch den Parameter $N$ in starkem Maße beeinflusst. Im statistischen Mittel wird die BER–Messung natürlich besser, wenn man $N$ erhöht.
• Es besteht jedoch kein deterministischer Zusammenhang zwischen der Anzahl der simulierten Bit und der Genauigkeit der BER–Messung, wie z. B. die Ergebnisse für $10 \cdot \lg \ E_{\rm B}/N_0 = 6 \ \rm dB$ zeigen:
• Bei $N = 6.4 \cdot 10^4\ (n_{\rm B} = 0.258 \cdot 10^{-2})$ ist die Abweichung vom tatsächlichen Wert $(0.239 \cdot 10^{-2})$ geringer als bei $N = 1.28 \cdot 10^5\ (n_{\rm B} = 0.272 \cdot 10^{-2})$.

(2)  Bei $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$, also $E_{\rm B} = N_0$, erhält man folgende Werte:

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.0786}{64000}}\hspace{0.1cm}\underline {\approx 1.1 \cdot10^{-3}}\hspace{0.05cm},$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} \sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.0786}{1600000}}\hspace{0.1cm}\underline {\approx 0.22 \cdot10^{-3}}\hspace{0.05cm}.$$

(3)  Hierfür ergeben sich mit $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$ folgende Werte:

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}} = \frac{0.0779-0.0786}{0.0786}\hspace{0.1cm}\underline {\approx -0.9\% }\hspace{0.05cm}$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} \varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.0782-0.0786}{0.0786}\hspace{0.1cm}\underline {\approx -0.5\% } \hspace{0.05cm}.$$

(4)  Aufgrund der kleineren Fehlerwahrscheinlichkeit ergeben sich nun kleinere Werte als in der Teilaufgabe (2):

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.336 \cdot 10^{-4}}{6.4 \cdot 10^{4}}}\hspace{0.1cm}\underline {\approx 2.3 \cdot 10^{-5}}\hspace{0.05cm},$$

$$ N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.336 \cdot 10^{-4}}{1.6 \cdot 10^{6}}}\hspace{0.1cm}\underline {\approx 0.46 \cdot10^{-5}}\hspace{0.05cm}.$$

(5)  Trotz der deutlich kleineren Streuung $\sigma_h$ ergeben sich für $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$ aufgrund der kleineren Fehlerwahrscheinlichkeit größere relative Abweichungen als für $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$:

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.625 \cdot 10^{-4} - 0.336 \cdot 10^{-4}}{0.336 \cdot 10^{-4}}\hspace{0.1cm}\underline { \approx 86\% } \hspace{0.05cm},$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.325 \cdot 10^{-4} - 0.336 \cdot 10^{-4}}{0.336 \cdot 10^{-4}}\hspace{0.1cm}\underline {\approx -3.3\%}\hspace{0.05cm}.$$

(6)  Die Anzahl der gemessenen Bitfehler sollte $n_{\rm B} \ge 100$ sein. Deshalb gilt näherungsweise (Rundungsfehler sind zu berücksichtigen):

$$n_{\rm B} = {p_{\rm B}}\cdot {N} > 100 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} > \frac{100}{1.6 \cdot 10^6} = 0.625 \cdot 10^{-4}\hspace{0.05cm}.$$

Daraus folgt weiter, dass bei der Simulation für $10 \cdot \lg \ E_{\rm B}/N_0\hspace{0.05cm}\underline{ = 8 \ \rm dB}$ noch ausreichend viele Bitfehler aufgetreten sind $(n_{\rm B} =315)$, während für $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$ im Mittel nur mehr $n_{\rm B} =52$ Fehler zu erwarten sind. Für diesen dB–Wert müsste etwa die doppelte Anzahl an Bits simuliert werden.