Difference between revisions of "Aufgaben:Exercise 3.7: Optimal Nyquist Equalization once again"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Lineare Nyquistentzerrung}} right|frame|Transversalfilterfrequenzgang Wir…“) |
|||
| Line 6: | Line 6: | ||
* binäre bipolare NRZ–Rechteckimpulse | * binäre bipolare NRZ–Rechteckimpulse | ||
:$$|H_{\rm S}(f)|= {\rm si}(\pi f T) \hspace{0.05cm},$$ | :$$|H_{\rm S}(f)|= {\rm si}(\pi f T) \hspace{0.05cm},$$ | ||
| − | * Koaxialkabel mit Kabeldämpfung $a_* = 9.2 \ {\rm Np} (\approx 80 \ \dB)$: | + | * Koaxialkabel mit Kabeldämpfung $a_* = 9.2 \ {\rm Np} (\approx 80 \ \rm dB)$: |
:$$|H_{\rm K}(f)|= {\rm exp}\left [ -9.2 | :$$|H_{\rm K}(f)|= {\rm exp}\left [ -9.2 | ||
\cdot \sqrt{2 \cdot |f| \cdot T} \right ]\hspace{0.05cm},$$ | \cdot \sqrt{2 \cdot |f| \cdot T} \right ]\hspace{0.05cm},$$ | ||
Revision as of 14:21, 30 October 2017
Wir gehen bei dieser Aufgabe von folgenden Voraussetzungen aus:
- binäre bipolare NRZ–Rechteckimpulse
- $$|H_{\rm S}(f)|= {\rm si}(\pi f T) \hspace{0.05cm},$$
- Koaxialkabel mit Kabeldämpfung $a_* = 9.2 \ {\rm Np} (\approx 80 \ \rm dB)$:
- $$|H_{\rm K}(f)|= {\rm exp}\left [ -9.2 \cdot \sqrt{2 \cdot |f| \cdot T} \right ]\hspace{0.05cm},$$
- optimaler Nyquistentzerrer, bestehend aus Matched–Filter und Transversalfilter:
- $$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f)\hspace{0.2cm}{\rm mit}$$
- $$H_{\rm MF}(f) = H_{\rm S}^{\star}(f) \cdot H_{\rm K}^{\star}(f)\hspace{0.05cm},\hspace{0.2cm} H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$
Hierbei bezeichnet $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ das Produkt von Sender– und Kanalfrequenzgang.
Wegen der Nyquistentzerrung ist das Auge maximal geöffnet. Für die Fehlerwahrscheinlichkeit gilt:
- $$p_{\rm S} \left ( = p_{\rm U} \right ) = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right ) \hspace{0.05cm}.$$
Die normierte Störleistung am Entscheider ist durch folgende Gleichungen gegeben:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \hspace{0.05cm},$$
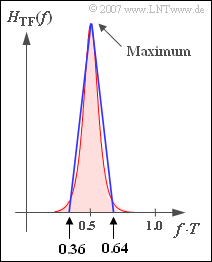
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f = T \cdot \int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \hspace{0.05cm}.$$
Die Gültigkeit dieser Gleichung ergibt sich aus der Periodizität des Transversalfilterfrequenzgangs. In der Grafik erkennt man die normierte Störleistung als die rot hinterlegte Fläche. Näherungsweise kann die normierte Störleistung durch die in der Grafik blau eingezeichnete Dreieckfläche berechnet werden.
Hinweis:
- Die Aufgabe bezieht sich auf das Kapitel Lineare Nyquistentzerrung.
- Zur Bestimmung der Fehlerwahrscheinlichkeit können Sie das folgende interaktive Berechnungsmodul nutzen: Gaußsche Fehlerfunktion
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)