Aufgaben:Exercise 3.7Z: Regenerator Field Length

• Return to book

Ergebnisse einer Systemsimulation

Per Simulation wurde gezeigt, dass zwischen dem sog. Systemwirkungsgrad $\eta$ sowie der charakteristischen Kabeldämpfung $a_*$ eines Koaxialkabels – beide in dB aufgetragen – etwa ein linearer Zusammenhang besteht, wenn die charakteristische Kabeldämpfung hinreichend groß ist ($a_* ≥ 40 \ \rm dB$):

$$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} \hspace{0.05cm}.$$

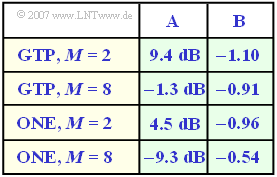
In der Tabelle sind für vier beispielhafte Systemvarianten

• impulsinterferenzbehaftetes System mit Gaußtiefpass (GTP, siehe Kapitel 3.4) bzw. optimale Nyquistentzerrung (ONE, siehe Kapitel 3.5)
• jeweils Binärsystem ($M = 2$) und Oktalsystem ($M = 8$)

die empirisch gefundenen Gleichungskoeffizienten $A$ und $B$ angegeben.

Für einen gegebenen Wert $a_*$ (und damit eine feste Kabellänge) ist ein System um so besser, je größer der Systemwirkungsgrad ist.

Für die Berecnung der Regeneratorfeldlänge (Abstand zweier Zwischenverstärker) ist zu beachten, dass

• die ungünstigste Fehlerwahrscheinlichkeit nicht größer sein soll als $10^{\rm –10}$, woraus sich der minimale Sinkenstörabstand ergibt:

$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} \approx 16.1\,{\rm dB} \hspace{0.05cm},$$

• das logarithmierte Verhältnis von Sendeenergie (pro Bit) und AWGN–Rauschleistungsdichte ca. $100 \ \rm dB$ beträgt, zum Beispiel:

$$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$

$$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}}= 10 \cdot {\rm lg} \hspace{0.1cm} \frac{9\,{\rm V^2} } {9 \cdot 10^{-19}\,{\rm V^2/Hz} \cdot 10^{-9}\,{\rm 1/s}} = 100\,{\rm dB} \hspace{0.05cm},$$

• ein Normalkoaxialkabel mit den Abmessungen $2.6 \ \rm mm$ (innen) und $9.5 \ \rm mm$ (außen) eingesetzt werden soll, bei dem der folgende Zusammenhang gültig ist:

$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} \hspace{0.05cm}.$$

Hierbei bezeichnet $a_*$ die charakteristische Dämpfung bei der halben Bitrate – im Beispiel bei $500 \ \rm MHz$ – und $l$ die Kabellänge.

Hinweis:

• Die Aufgabe bezieht sich auf das Kapitel Lineare Nyquistentzerrung.

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	Das System (ONE, $M = 8$) ist für beliebiges $a_*$ am besten
	Das System (GTP, $M = 2$) ist für $a_* ≥ 40 \ \rm dB$ am schlechtesten.

2

Ab welcher Kabeldämpfung ist (GTP, $M = 8$) besser als (ONE, $M = 2$)?

$a_{\rm *, \ Grenz}$ = $\ \rm dB$

3

Welchen Minimalwert $\eta_{\rm min}$ darf der Systemwirkungsgrad nicht unterschreiten?

$10 \cdot {\rm lg} \eta_{\rm min}$ = $\ \rm dB$

4

Welche Länge darf das Koaxialkabel bei (ONE, $M = 8$) maximal besitzen?

${\rm ONE,} \ M = 8 \text{:} \hspace{0.4cm} l_{\rm max}$ = $\ \rm km$

5

Welche Länge darf das Koaxialkabel bei (GTP, $M = 2$) maximal besitzen?

${\rm GTP,} \ M = 2 \text{:} \hspace{0.4cm} l_{\rm max}$ = $\ \rm km$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)