Difference between revisions of "Aufgaben:Exercise 1.6Z: Two Optimal Systems"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Optimierung der Basisbandübertragungssysteme }} [[File:|right|]] ===Fragebogen=== <quiz display=simpl…“) |
|||
| Line 4: | Line 4: | ||
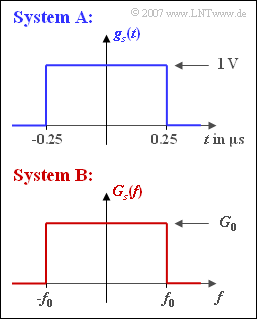
| − | [[File:|right|]] | + | [[File:P_ID1293__Dig_Z_1_6.png|right|frame|Optimalsysteme im Zeit- und Frequenzbereich]] |
| + | Betrachtet werden zwei binäre Übertragungssysteme '''A''' und '''B''', die bei einem AWGN–Kanal mit Rauschleistungsdichte $N_{0}$ das gleiche Fehlerverhalten aufweisen. In beiden Fällen gilt für die Bitfehlerwahrscheinlichkeit: | ||
| + | :$$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$ | ||
| + | Das System '''A''' verwendet den NRZ–Sendegrundimpuls $g_{s}(t)$ gemäß der oberen Skizze mit der Amplitude $s_{0} = 1 \ \rm V$ und der Dauer $T = 0.5\ \mu s$. Dagegen besitzt das System '''B''', das mit der gleichen Bitrate wie das System A arbeiten soll, ein rechteckförmiges Sendegrundimpulsspektrum: | ||
| + | :$$G_s(f) = \left\{ \begin{array}{c} G_0 \\ | ||
| + | 0 \\ \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm{f\ddot{u}r}} | ||
| + | \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} | ||
| + | |f| < f_0 \hspace{0.05cm}, \\ | ||
| + | |f| > f_0 \hspace{0.05cm}.\\ | ||
| + | \end{array}$$ | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | |||
| + | Diese Aufgabe bezieht sich auf das [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme|Optimierung der Basisbandübertragungssysteme]] des vorliegenden Buches. Beachten Sie bitte, dass hier die Impulsamplitude in „Volt” angegeben ist, so dass die mittlere Energie pro Bit $(E_{\rm B})$ die Einheit $„V^{2}/Hz”$ aufweist. | ||
| + | |||
| Line 10: | Line 25: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {Mit welcher Bitrate arbeiten die beiden Systeme? | ||
| + | |type="{}"} | ||
| + | $R \ = \ $ { 2 3% } $\ \rm Mbit/s$ | ||
| + | |||
| + | {Berechnen Sie die Energie pro Bit für das System '''A'''. | ||
| + | |type="{}"} | ||
| + | $E_{\rm B} \ = \ $ { 5 3% } $\ \cdot 10^{-7} \ \rm V^{2}/Hz$ | ||
| + | |||
| + | {Welche Aussagen gelten für die Empfangsfilter der Systeme '''A''' und '''B'''? | ||
|type="[]"} | |type="[]"} | ||
| − | + | +Bei System '''A''' hat $H_{\rm E}(f)$ einen si–förmigen Verlauf. | |
| − | + | + | +Bei System '''B''' ist $H_{\rm E}(f)$ ein idealer, rechteckförmiger Tiefpass. |
| + | -$H_{\rm E}(f)$ lässt sich bei System '''B''' durch einen Integrator realisieren. | ||
| + | {Für welche Grenzfrequenz $f_{0}$ weist das System '''B''' die Symboldauer $T$ auf? | ||
| + | |type="{}"} | ||
| + | $f_{0} \ = \ ${ 1 3% } $\ \rm MHz$ | ||
| − | { | + | {Wie groß ist die konstante Höhe $G_{0}$ des Spektrums von '''B''' zu wählen, damit sich die gleiche Energie pro Bit ergibt wie bei System '''A'''? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $G_{0} \ = \ $ { 5 3% } $\ \cdot 10^{-7} \ \rm V/Hz$ |
| + | {Wäre eines der beiden Systeme auch bei Spitzenwertbegrenzung geeignet? | ||
| + | |type="[]"} | ||
| + | +System '''A''', | ||
| + | - System '''A'''. | ||
Revision as of 23:43, 5 November 2017
Betrachtet werden zwei binäre Übertragungssysteme A und B, die bei einem AWGN–Kanal mit Rauschleistungsdichte $N_{0}$ das gleiche Fehlerverhalten aufweisen. In beiden Fällen gilt für die Bitfehlerwahrscheinlichkeit:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$
Das System A verwendet den NRZ–Sendegrundimpuls $g_{s}(t)$ gemäß der oberen Skizze mit der Amplitude $s_{0} = 1 \ \rm V$ und der Dauer $T = 0.5\ \mu s$. Dagegen besitzt das System B, das mit der gleichen Bitrate wie das System A arbeiten soll, ein rechteckförmiges Sendegrundimpulsspektrum:
- $$G_s(f) = \left\{ \begin{array}{c} G_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |f| < f_0 \hspace{0.05cm}, \\ |f| > f_0 \hspace{0.05cm}.\\ \end{array}$$
Hinweis:
Diese Aufgabe bezieht sich auf das Optimierung der Basisbandübertragungssysteme des vorliegenden Buches. Beachten Sie bitte, dass hier die Impulsamplitude in „Volt” angegeben ist, so dass die mittlere Energie pro Bit $(E_{\rm B})$ die Einheit $„V^{2}/Hz”$ aufweist.
Fragebogen
Musterlösung