Difference between revisions of "Aufgaben:Exercise 4.3: Different Frequencies"
From LNTwww
| Line 21: | Line 21: | ||
{Beschreiben Sie die Signalmenge $\{s_i(t)\}, 0 ≤ i ≤ 4$ möglichst kompakt. Welche Beschreibungsform ist richtig? | {Beschreiben Sie die Signalmenge $\{s_i(t)\}, 0 ≤ i ≤ 4$ möglichst kompakt. Welche Beschreibungsform ist richtig? | ||
|type="[]"} | |type="[]"} | ||
| − | - $s_i(t) = A \cdot \cos {2\pi i \cdot t/T}$. | + | - $s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$. |
| − | + $s_i(t) = A \cdot \cos {2\pi i \cdot t/T}$ für $0 ≤ t < T$, sonst $0$. | + | + $s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$ für $0 ≤ t < T$, sonst $0$. |
| − | - $s_i(t) = A \cdot \cos {2\pi i – i \cdot \pi/2}$ für $0 ≤ t < T$, sonst $0$. | + | - $s_i(t) = A \cdot \cos {(2\pi i \, – \, i \cdot \pi/2)}$ für $0 ≤ t < T$, sonst $0$. |
{Geben Sie die Anzahl $N$ der erforderlichen Basisfunktionen an. | {Geben Sie die Anzahl $N$ der erforderlichen Basisfunktionen an. | ||
| Line 38: | Line 38: | ||
|type="[]"} | |type="[]"} | ||
- $\varphi_1(t) = s_1(t)$, | - $\varphi_1(t) = s_1(t)$, | ||
| − | - $\varphi_1(t) = (1/T)^{\rm 0.5} \cdot \cos {2\pi t/T}$ für $0 ≤ t < T$, außerhalb $0$. | + | - $\varphi_1(t) = (1/T)^{\rm 0.5} \cdot \cos {(2\pi t/T)}$ für $0 ≤ t < T$, außerhalb $0$. |
| − | + $\varphi_1(t) = (2/T)^{\rm 0.5} \cdot \cos {2\pi t/T}$ für $0 ≤ t < T$, außerhalb $0$. | + | + $\varphi_1(t) = (2/T)^{\rm 0.5} \cdot \cos {(2\pi t/T)}$ für $0 ≤ t < T$, außerhalb $0$. |
</quiz> | </quiz> | ||
Revision as of 12:41, 6 November 2017
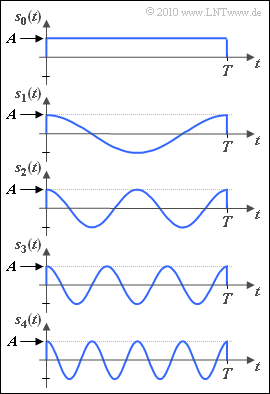
In der Grafik sind $M = 5$ Signale $s_i(t)$ dargestellt. Entgegen der Nomenklatur im Theorieteil sind für die Laufvariable $i$ die $0, \ ... \ , M–$ möglich. Anzumerken ist:
- Alle Signale sind zeitbegrenzt auf $0$ bis $T$; damit ist auch die Energie aller Signale endlich.
- Das Signal $s_1(t)$ hat die Periodendauer $T_0 = T$. Die Frequenz ist damit gleich $f_0 = 1/T$.
- Die Signale $s_i(t)$, $i ≠ 0$, sind Cosinusschwingungen mit der Frequenz $i \cdot f_0$. Dagegen ist $s_0(t)$ zwischen $0$ und $T$ konstant.
- Der Maximalwert aller Signale ist $A$ und es gilt $|s_i(t)| ≤ A$.
Gesucht sind in dieser Aufgabe die $N$ Basisfunktionen, die hier entgegen der bisherigen Beschreibung im Theorieteil mit $j = 0, \ ... \ , N–1$ durchnummeriert werden.
Hinweis:
- Die Aufgabe bezieht sich auf das Kapitel Signale, Basisfunktionen und Vektorräume.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.