Aufgaben:Exercise 4.5: Irrelevance Theorem

• Return to book

Betrachtetes Optimalsystem mit Detektor und Entscheider

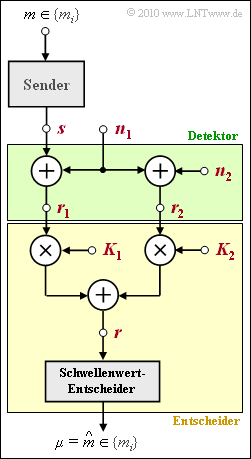
Untersucht werden soll das durch die Grafik vorgegebene Kommunikationssystem. Die binäre Nachricht $m ∈ \{m_0, m_1\}$ mit gleichen Auftrittswahrscheinlichkeiten

$${\rm Pr} (m_0 ) = {\rm Pr} (m_1 ) = 0.5$$

wird durch die beiden Signale

$$s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$$

dargestellt, wobei die Zuordnungen $m_0 ⇔ s_0$ und $m_1 ⇔ s_1$ eineindeutig sind. Der Detektor (im Bild grün hinterlegt) liefert zwei Entscheidungswerte

$$r_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s + n_1\hspace{0.05cm},$$

$$r_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} n_1 + n_2\hspace{0.05cm},$$

aus denen der Entscheider die Schätzwerte $\mu ∈ \{m_0, m_1\}$ für die gesendete Nachricht $m$ bildet. Der Entscheider beinhaltet zwei Gewichtungsfaktoren $K_1$ und $K_2$, eine Summationsstelle und einen Schwellenwertentscheider mit der Schwelle bei $0$.

Betrachtet werden in dieser Aufgabe drei Auswertungen:

• Entscheidung basierend auf $r_1$ ($K_1 ≠ 0, K_2 = 0$),
• Entscheidung basierend auf $r_2$ ($K_1 = 0, K_2 ≠ 0$),
• gemeinsame Auswertung von $r_1$ und $r_2$ ($K_1 ≠ 0, K_2 ≠ 0$).

Die zwei Rauschquellen $n_1$ und $n_2$ seien voneinander unabhängig und auch unabhängig vom Sendesignal $s ∈ \{s_0, s_1\}$. $n_1$ und $n_2$ können jeweils durch AWGN–Rauschquellen (weiß, gaußverteilt, mittelwertfrei, Varianz $\sigma^2 = N_0/2$) modelliert werden. Verwenden Sie für numerische Berechnungen die Werte

$$E_s = 8 \cdot 10^{-6}\,{\rm Ws}\hspace{0.05cm},\hspace{0.2cm}N_0 = 10^{-6}\,{\rm W/Hz} \hspace{0.05cm}.$$

Die Komplementäre Gaußsche Fehlerfunktion liefert folgende Ergebnisse:

$${\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{1.35cm}{\rm Q}(2^{0.5}) = 0.786 \cdot 10^{-1}\hspace{0.05cm},\hspace{1.1cm}{\rm Q}(2) = 0.227 \cdot 10^{-1}\hspace{0.05cm},$$

$${\rm Q}(2 \cdot 2^{0.5}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.234 \cdot 10^{-2}\hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4) = 0.317 \cdot 10^{-4} \hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4 \cdot 2^{0.5}) = 0.771 \cdot 10^{-8}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Struktur des optimalen Empfängers dieses Buches.
• Insbesondere wird hier auf das Theorem der Irrelevanz Bezug genommen, daneben aber auch auf den Optimalen Empfänger für den AWGN–Kanal.
• Weitere Informationen zu den für diese Aufgabe relevanten Themen finden Sie unter folgenden Links:
  • Entscheidungsregeln für MAP– und ML–Empfänger,
  • Realisierung als Korrelationsempfänger bzw. Matched–Filter–Empfänger,
  • Bedingte Gaußsche Wahrscheinlichkeitsdichtefunktionen.

• Für die Fehlerwahrscheinlichkeit eines Systems $r = s + n$ (wegen $N = 1$ sind hier $s, n, r$ Skalare) gilt

$$p_{\rm S} = {\rm Pr} ({\rm Symbolfehler} ) = {\rm Q} \left ( \sqrt{{2 E_s}/{N_0}}\right ) \hspace{0.05cm},$$

1. wobei ein binäres Nachrichtensignal $s ∈ \{s_0, s_1\}$ mit

$$s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$$

1. vorausgesetzt wird und die zweiseitige Rauschleistungsdichte von $n$ konstant gleich $\sigma^2 = N_0/2$ ist.

Fragebogen

1

Welche Aussagen gelten hier bezüglich des Empfängers?

	Der ML–Empfänger ist hier besser als der MAP–Empfänger.
	Der MAP–Empfänger ist hier besser als der ML–Empfänger.
	Beide Empfänger liefern hier das gleiche Ergebnis.

2

Welche Fehlerwahrscheinlichkeit ergibt sich mit $K_2 = 0$?

$K_2 = 0 \text{:} \hspace{0.2cm} {\rm Pr(Symbolfehler)}$ = $\ \cdot 10^{\rm –4}$

3

Welche Fehlerwahrscheinlichkeit ergibt sich mit $K_1 = 0$?

$K_1 = 0 \text{:} \hspace{0.2cm} {\rm Pr(Symbolfehler)}$ = $\ \cdot 10^0$

4

Kann durch die Verwendung von $r_1$ und $r_2$ eine Verbesserung erzielt werden?

	Ja.
	Nein.

5

Welche Gleichungen gelten für den Schätzwert ($\mu$) bei AWGN–Rauschen?

	$\mu = {\rm arg \ min} \, [(\rho_1 + \rho_2) \cdot s_i]$,
	$\mu = {\rm arg \ min} \, [(\rho_2 \, – 2 \rho_1) \cdot s_i]$,
	$\mu = {\rm arg \ max} \, [(\rho_1 + \rho_2/2) \cdot s_i]$.

6

Wie kann diese Regel mit dem vorgegebenen Entscheider (Schwelle bei $0$) exakt umgesetzt werden? Es gelte $K_1 = 1$.

$K_2$ =

7

Welche (minimale) Fehlerwahrscheinlichkeit ergibt sich mit der Realisierung entsprechend der Teilaufgabe (6)?

${\rm Minimum \ [Pr(Symbolfehler)]}$ = $\ \cdot 10^{\rm –8}$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)