Aufgaben:Exercise 1.08: Comparison of ASK and BPSK

• Return to book

Fehlerwahrscheinlichkeiten von ASK und BPSK

Die Bitfehlerwahrscheinlichkeiten der Modulationsarten $Amplitude Shift Keying$ (ASK) sowie $Binary Shift Keying$ (BPSK) werden oft durch die beiden folgenden Gleichungen angegeben:

$$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$

$$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$

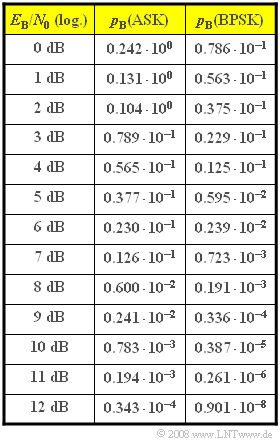
Diese beiden Gleichungen sind in der beigefügten Tabelle ausgewertet. Dabei gilt:

• $E_{\rm B}$ gibt die mittlere Energie pro Bit an.
• $N_{0}$ ist die Rauschleistungsdichte.
• Zwischen den Fehlerfunktionen Q$(x)$ und erfc$(x)$ besteht ein fester Zusammenhang.

Anzumerken ist, dass diese Gleichungen nicht allgemein gelten, sondern nur unter gewissen idealisierten Bedingungen. Diese Voraussetzungen sollen in dieser Aufgabe herausgearbeitet werden.

Hinweis:

Die Aufgabe gehört zum Themengebiet von Lineare digitale Modulation – Kohärente Demodulation.

Fragebogen

1

Welcher Zusammenhang besteht zwischen Q$(x)$ und erfc$(x)$?

	Es gilt Q$(x) = 2\ \cdot$ erfc$(x)$,
	Es gilt Q$(x) = 0.5\ \cdot$ erfc$(x/20.5)$,
	Es gilt erfc$(x) = 0.5\ \cdot$ Q$(x/20.5)$.

2

Wann gelten die angegebenen Fehlerwahrscheinlichkeits–Gleichungen?

	Sie gelten nur für den AWGN–Kanal.
	Sie gelten nur für Matched–Filter–Empfänger (oder Varianten).
	Die Gleichungen berücksichtigen Impulsinterferenzen.
	Die Gleichungen gelten nur bei rechteckförmigen Signalen.

3

Wie lauten die Fehlerwahrscheinlichkeiten für $10 \cdot \lg \ E_{\rm B}/N_{0} = 12\ \rm dB$?

$ p_{\rm ASK} \ = \ $ $\ \cdot 10^{-4}$

$ p_{\rm BPSK} \ = \ $ $\ \cdot 10^{-8}$

4

Welche Fehlerwahrscheinlichkeiten ergeben sich für $E_{\rm B}/N_{0} = 8$?

$ p_{\rm ASK} \ = \ $ $\ \cdot 10^{-2}$

$ p_{\rm BPSK} \ = \ $ $\ \cdot 10^{-4}$

5

Die Fehlerwahrscheinlichkeit soll nicht größer werden als $10^{-8}$. Wie groß ist das erforderliche $10 \cdot \lg \ E_{\rm B}/N_{0}$ bei ASK?

$(E_{\rm B}/N_{0})_{\rm min} \ = \ $ $\ \rm dB $

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)