Aufgaben:Exercise 4.14: 8-PSK and 16-PSK

• Return to book

Signalraumkonstellation der 8–PSK und 16–PSK

Betrachtet wird nun eine Signale $s_i(t)$, die auf den Zeitbereich $0 ≤ t ≤ T$ begrenzt ist. Der Index $i$ durchläuft die Werte $0, \ ... \ , M–1$:

$$s_i(t) = A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) \hspace{0.05cm}.$$

Es handelt sich hierbei um eine Phasenmodulation mit $M$ Signalformen. Man nennt dieses Modulationsverfahren auch M–PSK. $M$ ist meist eine Zweierpotenz.

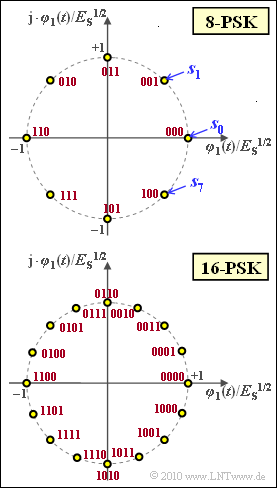
Die Grafik zeigt die Signalraumkonstellation für $M = 8$ (oben) und $M = 16$ (unten). Alle Signalraumpunkte haben gleiche Energie $||\boldsymbol{s}_i||^2 = E_{\rm S}$ („mittlere Symbolenergie”).

Die exakte Berechnung der Fehlerwahrscheinlichkeit ist für $M ≠ 2$ schwierig. Angegeben werden kann dagegen stets die sogenannte Union Bound als obere Schranke für die Symbolfehlerwahrscheinlichkeit ($p_{\rm UB} ≥ p_{\rm S}$):

$$ p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) = 2 \cdot {\rm Q} \left (\sqrt{ \frac{ d^2}{ 2 N_0}}\right ) \hspace{0.05cm}.$$

Hierbei bezeichnen:

• $d$ ist der Abstand zwischen zwei benachbarten Punkten, zum Beispiel zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$. Verläuft die Entscheidungsgrenze senkrecht zur Verbindungslinie von $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ genau mittig, so ist $d/2$ der Abstand von $\boldsymbol{s}_0$ bzw. $\boldsymbol{s}_1$ von dieser Entscheidungsgrenze.
• Die Varianz des AWGN–Rauschens ist $\sigma_n^2 = N_0/2$.
• Der Faktor $2$ in obiger Grenze berücksichtigt, dass für $M > 2$ jeder Signalraumpunkt in zwei Richtungen verfälscht werden kann, zum Beispiel bei der 8–PSK das Symbol $\boldsymbol{s}_0$ in das Symbol $\boldsymbol{s}_1$ oder in das Symbol $\boldsymbol{s}_7$.
• ${\rm Q}(x)$ ist die komplementäre Gaußsche Fehlerfunktion, für die folgende Näherung gilt:

$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

In der letzten Teilaufgabe geht es um die Bitfehlerwahrscheinlichkeit. Für diese wurde im Theorieteil unter der Voraussetzung eines Graycodes folgende Schranke angegeben:

$$p_{\rm B} \le \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$

Diese Gleichung ist allerdings nur für $M > 4$ anzuwenden. Dagegen ergibt sich

• für $M = 2$ aus der Identität mit der BPSK, und
• für $M = 4$ aus der Tatsache, dass die 4–PSK mit der 4–QAM identisch ist,

die exakte Lösung

$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels Trägerfrequenzen mit kohärenter Demodulation und bezieht sich insbesondere auf die Seite 7.
• Bei der Lösung der Aufgabe können Sie folgende Gleichungen verwenden:

$$\cos(\alpha + \beta) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(\alpha ) \cdot \cos( \beta) - \sin(\alpha ) \cdot \sin( \beta)\hspace{0.05cm}, \hspace{0.25cm} 1 - \cos(2\alpha ) = \sin^2(\alpha )\hspace{0.05cm},$$

$$ \int_{0}^{T} \cos^2 ( 2\pi f_{\rm T}t) \,{\rm d} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{0.15cm}{\rm falls}\hspace{0.15cm} f_{\rm T} >> 1/T \hspace{0.05cm}.$$

• Die Zuordnung der 8 bzw. 16 Symbole zu Binärfolgen der Länge 3 bzw. 4 nach der Graycodierung kann der Grafik entnommen werden (rote Beschriftung).

Fragebogen

1

Wie lauten die Basisfunktionen bei der Bandpassdarstellung? $\varphi_1(t)$ und $\varphi_2(t)$ seien jeweils auf den Bereich $0 ≤ t ≤ T$ begrenzt

	$\varphi_1(t) = \cos {(2\pi f_{\rm T}t)}$,
	$\varphi_1(t) = \sqrt {2/T} \cdot \cos {(2\pi f_{\rm T}t)}$,
	$\varphi_2(t) = E_{\rm S} \cdot \sin {(2\pi f_{\rm T}t)}$,
	$\varphi_2(t) = \, –\sqrt {2/T} \cdot \sin {(2\pi f_{\rm T}t)}$.

2

Wie lauten der Inphase– und der Quadraturanteil des Signalraumpunktes $\boldsymbol{s}_i$? Welche Aussagen treffen zu?

	$s_{\rm I \it i} = \sqrt {E_{\rm S}} \cdot \cos {(2\pi \cdot i/M)}$,
	$s_{\rm I \it i} = \sqrt {E_{\rm S}} \cdot \sin {(2\pi \cdot i/M)}$,
	$s_{\rm Q \it i} = \sqrt {E_{\rm S}} \cdot \cos {(2\pi \cdot i/M)}$,
	$s_{\rm Q \it i} = \sqrt {E_{\rm S}} \cdot \sin {(2\pi \cdot i/M)}$.

3

Wie groß ist der Abstand $d$ zwischen zwei benachbarten Signalraumpunkten? Welche Werte ergeben sich für $M = 8$ bzw. $M = 16$?

$M = 8 \text{:} \hspace{0.2cm} d$ = $\ \cdot \sqrt {E_{\rm S}}$

$M = 16 \text{:} \hspace{0.2cm} d$ = $\ \cdot \sqrt {E_{\rm S}}$

4

Welcher Wert ergibt sich für die Union Bound ($p_{\rm UB}$) mit $E_{\rm S}/N_0 = 50$.

$M = 8 \text{:} \hspace{0.2cm} p_{\rm UB}$ = $\ \cdot 10^{\rm –4}$

$M = 16 \text{:} \hspace{0.2cm} p_{\rm UB}$ = $\ \cdot 10^{\rm –2}$

5

Gilt die Aussage: „$p_{\rm UB}$ nähert $p_{\rm S}$ um so genauer an, je größer $M$ ist”?

	JA.
	NEIN.

6

Welche Aussagen gelten hinsichtlich der Bitfehlerwahrscheinlichkeit $p_{\rm UB}$?

	$p_{\rm B}$ ist für $M = 2$ und $M = 4$ am kleinsten.
	$p_{\rm B}$ ist für $M = 8$ am kleinsten.
	$p_{\rm B}$ ist für $M = 16$ am kleinsten.
	$p_{\rm B}$ ist nicht der Hauptgrund, dass man höherstufige PSK einsetzt.

Musterlösung

Solution

(1)  Die Signalmenge kann im Bandpassbereich mit der angegebenen trigonometrischen Umformung wie folgt dargestellt werden:

$$s_i(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) =$$

$$ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \cos \left ( 2\pi f_{\rm T}t \right )- A \cdot \sin \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \sin \left ( 2\pi f_{\rm T}t \right )\hspace{0.05cm}.$$

Die jeweils ersten Terme in dieser Differenz führen zum Signalraumpunkt $\boldsymbol{s}_i$, die jeweils zweiten zu den Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$. Hierbei ist zu beachten, dass diese jeweils energienormiert sein müssen:

$$\int_{0}^{T} \varphi_1 ( t)^2 \,{\rm d} t = \int_{0}^{T} \left [K \cdot \cos( 2\pi f_{\rm T}t)\right ]^2 \,{\rm d} t = 1$$

$$\Rightarrow \hspace{0.3cm} \frac{K^2 \cdot T}{2} = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = \sqrt{2/T } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \varphi_1 ( t) = \sqrt{2/T } \cdot \cos( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$

Mit gleichem Rechenweg kommt man zur zweiten Basisfunkion:

$$\varphi_2 ( t) = -\sqrt{2/T } \cdot \sin( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$

Richtig sind somit die Lösungsvorschläge 2 und 4.

(2)  Unter Verwendung der eben berechneten Basisfunktionen kann die Signalmenge $s_i(t)$ wie folgt dargestellt werden (wiederum begrenzt auf den Bereich $0 ≤ t ≤ T$):

$$s_i(t) = A \cdot \sqrt{T/2 } \cdot \cos ( 2\pi \cdot i /M ) \cdot \varphi_1 ( t)+ A \cdot \sqrt{T/2 } \cdot \sin ( 2\pi \cdot i /M ) \cdot \varphi_2 ( t) \hspace{0.05cm}.$$

Mit der für alle $M$ Punkte gleichen Energie $E = 0.5 \cdot A^2 \cdot T$, die gleichzeitig die mittlere Signalenergie pro Symbol ($E_{\rm S}$) ist, lautet obige Gleichung

$$s_i(t) = s_{{\rm I}i} \cdot \varphi_1 ( t)+ s_{{\rm Q}i} \cdot \varphi_2 ( t)$$

$$\Rightarrow \hspace{0.3cm} s_{{\rm I}i} = \sqrt{E_{\rm S} }\cdot \cos ( 2\pi \cdot i /M )\hspace{0.05cm},\hspace{0.2cm} s_{{\rm Q}i} = \sqrt{E_{\rm S} }\cdot \sin ( 2\pi \cdot i /M )\hspace{0.05cm}. $$

Die in der Grafik auf der Angabenseite für $M = 8$ bzw. $M = 16$ skizzierten Signalraumpunkte lassen sich genau in dieser Weise darstellen. Richtig sind demzufolge die Lösungsvorschläge 1 und 4.

(3) 

Zur Abstandsberechnung bei 8-PSK

Da der Abstand von einem zum nächstgelegenen Punkt für alle $i$ gleich ist, können wir $d$ beispielsweise aus den Signalraumpunkten $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ berechnen. Betrachten Sie dabei die nachfolgende Skizze. Nach dem Satz von Pythagoras gilt:

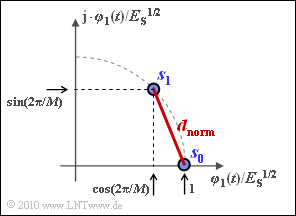
$$d_{\rm norm}^2 \hspace{-0.01cm}=\hspace{-0.01cm} \sin^2(\frac{2\pi}{M}) + [1- \cos(\frac{2\pi}{M})]^2 = $$

$$\hspace{-0.01cm}=\hspace{-0.01cm} 2 \cdot [1- \cos( \frac{2\pi}{M} )] = 4 \cdot \sin^2(\pi/M )\hspace{0.05cm} $$

$$\Rightarrow \hspace{0.2cm} d_{\rm norm}= 2 \cdot \sin({\pi}/{M }) $$

$$\Rightarrow \hspace{0.2cm} d = 2\sqrt {E_{\rm S}} \cdot \sin{\pi}/{M })\hspace{0.05cm}.$$

Daraus ergeben sich folgende Zahlenwerte:

$$M = 8\hspace{-0.09cm}: \hspace{0.2cm}d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.765} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm},$$

$$M = 16\hspace{-0.09cm}: \hspace{0.2cm} d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.390} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm}.$$

(4)  Mit dem Ergebnis aus (3) erhält man mit der vorne angegebenen Gleichung:

$$p_{\rm S} \le p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$

Mit $E_{\rm S}/N_0 = 50$ ⇒ $(2E_{\rm S}/N_0)^{\rm 0.5} = 10$ folgt daraus:

$$M = 8\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.383 )= 2 \cdot {\rm Q} ( 3.83 ) \approx \underline{1.4 \cdot 10^{-4}} \hspace{0.05cm},$$

$$ M = 16\hspace{-0.09cm}: \hspace{0.2cm} p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.195 )= 2 \cdot {\rm Q} ( 1.95 ) \approx \underline{6 \cdot 10^{-2}} \hspace{0.05cm}.$$

Anzumerken ist, dass die Fehlerwahrscheinlichkeit mit steigendem $M$ immer größer wird, wenn man – wie hier – von einem konstanten $E_{\rm S}/N_0$ ausgeht. Der günstigste Wert ergäbe sich für $M = 2$ (der Faktor $2$ der Union Bound ist dann nämlich nicht notwendig) zu

$$M = 2\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} = p_{\rm S} = {\rm Q} ( 10 ) \approx { 10^{-23}}.$$

Mehrstufige PSK würde also keinen Sinn machen, wenn es nicht andere Gründe für deren Anwendung gäbe, worauf in der Teilaufgabe (6) noch eingegangen wird.

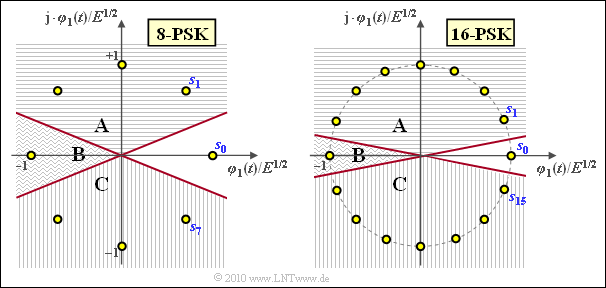
(5)  Richtig ist JA. Die Grafik zeigt die Konstellation für 8–PSK und 16–PSK, jeweils gültig unter der Annahme, dass $\boldsymbol{s}_0$ gesendet wurde. Die Höhenlinien der AWGN–WDF sind dann Kreise um $\boldsymbol{s}_0$.

Zur Interpretation der Union Bound bei M–PSK

Es gelten folgende Aussagen:

• Die tatsächliche Fehlerwahrscheinlichkeit $p_{\rm S}$ setzt sich aus den Anteilen A, B und C zusammen.
• Dagegen ergibt sich die „Union Bound” ($p_{\rm S}$) aus A + B (Verfälschung in das Symbol $\boldsymbol{s}_1$) plus B + C (Verfälschung in das Symbol $\boldsymbol{s}_{\it M–1}$).
• Damit gilt stets $p_{\rm S} = p_{\rm UB}$ – B. Der Anteil B ist aber um so kleiner, je größer $M$ ist.

(6)  Zur Überprüfung gehen wir beispielsweise von $p_{\rm B} = 10^{\rm –4}$ aus. Daraus folgt für $M = 2$ und $M = 4$:

$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) = 10^{-4}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sqrt{ { {2E_{\rm B}}}/{ N_0} } \approx 3.72 \hspace{0.05cm}.$$

Dagegen gilt mit der angegebenen Gleichung $M = 8$:

$$p_{\rm B} \hspace{-0.1cm} \ \le \ \hspace{-0.1cm} \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right )=$$

$$ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} \left ( \sqrt{3} \cdot 0.383 \cdot 3.72 \right ) \approx {2}/{3} \cdot {\rm Q} \left ( 2.46 \right ) \approx 0.46 \cdot 10^{-2} \hspace{0.05cm}.$$

Entsprechend erhält man für $M = 16$ ⇒ ${\rm ld} (M) = 4$:

$$p_{\rm B} = {2}/{4} \cdot {\rm Q} \left ( \sqrt{4} \cdot 0.195 \cdot 3.72 \right ) \approx {1}/{2} \cdot {\rm Q} \left ( 1.45 \right ) \approx 0.48 \cdot 10^{-1} \hspace{0.05cm}.$$

Richtig sind also die Aussagen 1 und 4. Der wesentliche Vorteil einer höherstufigen PSK ist also nicht die niedrigere Bitfehlerrate, sondern der geringere Bedarf an der sehr teueren Ressource „Bandbreite”. Außerdem ist zu beachten, dass die Ergebnisse völlig anders sind, wenn ein (stark) verzerrender Kanal vorliegt, wie in der Leitungsgebundenen Übertragungstechnik üblich.