Aufgaben:Exercise 4.13: Four-level QAM

• Return to book

Signalraumkonstellation der 4–QAM

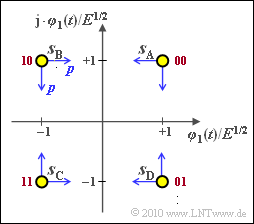
Wir betrachten nun eine Quadraturamplitudenmodulation mit $M = 4$ Symbolen und den (normierten) Signalraumpunkten

$$\boldsymbol{ s}_{\rm A} = (+1, +1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm B} = (-1, +1)\hspace{0.05cm},$$

$$ \boldsymbol{ s}_{\rm C} = (-1, -1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm D} = (+1, -1) \hspace{0.05cm}.$$

Die Symbole sind gleichwahrscheinlich. Damit kann man zur Berechnung der mittleren Symbolfehlerwahrscheinlichkeit auf die Mittelung verzichten.

Beispielsweise gilt:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) \hspace{0.05cm}.$$

Die Zuordnung der Symbole zu Bitdupeln kann ebenfalls der Grafik (rote Beschriftungen) entnommen werden. Hierbei ist die Graycodierung vorausgesetzt.

Hinweise:

• Die Aufgabe bezieht sich auf die Theorieseite 6 von Kapitel 4.4.
• Für die Teilaufgabe (4) ist der (zeitdiskrete) AWGN–Kanal mit der Varianz $\sigma_n^2 = N_0/2$ vorausgesetzt.
• Für die Wahrscheinlichkeit, dass durch dessen Rauschsignal $n$ ein Symbol horizontal oder vertikal verfälscht wird, gilt mit der komplementären Gaußschen Fehlerfunktion:

$$p = {\rm Pr}( n < -x_0) = {\rm Pr}( n > + x_0) = {\rm Q}(x_0 / \sigma_n) \hspace{0.05cm}.$$

Fragebogen

1

Geben Sie als obere Schranke für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ die „Union Bound” an ($p_{\rm UB} ≥ p_{\rm S}$). Es gelte $p = 0.1$.

$p_{\rm UB}$ =

2

Wie groß ist die tatsächliche Symbolfehlerwahrscheinlichkeit?

$p_{\rm S}$ =

3

Wie groß ist die Bitfehlerwahrscheinlichkeit bei Graycodierung?

$p_{\rm B}$ =

4

Welcher Zusammenhang besteht zwischen $p_{\rm B}$ und $E_{\rm B}/N_0$?

	$p_{\rm B} = {\rm Q}(\sqrt {E_{\rm B}/N_0})$,
	$p_{\rm B} = {\rm Q}(\sqrt {2E_{\rm B}/N_0})$,
	$p_{\rm B} = {\rm Q}(\sqrt {E_{\rm B}/2N_0})$,

Musterlösung

Solution

(1)  Die „Union Bound” ist eine obere Schranke für die mittlere Symbolfehlerwahrscheinlichkeit. Für letztere gilt:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {\rm Pr}( {\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet})= $$

$$ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) \hspace{0.05cm}.$$

Dagegen gilt für die (verbesserte) „Union Bound” im vorliegenden Beispiel:

$$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) +$$

$$ \hspace{-0.1cm} \ + \ \hspace{-0.1cm}{\rm Pr}( \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) = 2p = \underline{0.2} \hspace{0.05cm}.$$

(2)  Die beiden Wahrscheinlichkeiten, aus der sich die „Union Bound” additiv zusammensetzt, lassen sich geometrisch wie folgt deuten:

• ${\rm Pr}(\boldsymbol{s}_{\rm B} \cup \boldsymbol{s}_{\rm C} | \boldsymbol{s}_{\rm A})$ ist die Wahrscheinlichkeit, dass der Empfangspunkt in der linken Halbebene liegt  ⇒  die AWGN–Rauschkomponente $n_1$ ist negativ und betragsmäßig größer als $E^{\rm 1/2}$.
• ${\rm Pr}(\boldsymbol{s}_{\rm C} \cup \boldsymbol{s}_{\rm D} | \boldsymbol{s}_{\rm A})$ ist die Wahrscheinlichkeit, dass der Empfangspunkt in der unteren Halbebene liegt  ⇒  die AWGN–Rauschkomponente $n_2$ ist negativ und betragsmäßig größer als $E^{\rm 1/2}$.

Das bedeutet, dass die „Union Bound” den dritten Quadranten zweimal berücksichtigt. Diesen Fehler kann man hier relativ einfach kompensieren:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm UB} - {\rm Pr}( \boldsymbol{ s}_{\rm C} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) = $$

$$ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 p - {\rm Pr}\left [ ( n_1 < -\sqrt{E})\cap ( n_2 < -\sqrt{E})\right ] = 2p - p^2 = \underline{0.19} \hspace{0.05cm}.$$

Hierbei ist berücksichtigt, dass die Rauschkomponenten $n_1$ und $n_2$ voneinander unabhängig sind.

(3)  Wie in der Teilaufgabe (2) nachgewiesen, gelten für die einzelnen Verfälschungswahrscheinlichkeiten:

• Quadrant 2: ${\rm Pr}(\boldsymbol{s}_{\rm B} \ {\rm empfangen} \ | \ \boldsymbol{s}_{\rm A} \ {\rm gesendet}) = 0.09$,
• Quadrant 3: ${\rm Pr}(\boldsymbol{s}_{\rm C} \ {\rm empfangen} \ | \ \boldsymbol{s}_{\rm A} \ {\rm gesendet}) = 0.01$,
• Quadrant 4: ${\rm Pr}(\boldsymbol{s}_{\rm D} \ {\rm empfangen} \ | \ \boldsymbol{s}_{\rm A} \ {\rm gesendet}) = 0.09$.

Für die mittlere Bitfehlerwahrscheinlichkeit erhält man somit:

$$p_{\rm B} = { 1}/{ 2} \cdot \left [ 1 \cdot 0.09 + 2 \cdot 0.01 + 1 \cdot 0.09\right ]= \underline{0.1} = p \hspace{0.05cm}.$$

Hierbei ist berücksichtigt, dass der Quadrant 2 und der Quadrant 4 jeweils nur zu einem Bitfehler führt, der Quadrant 3 dagegen zu zweien. Der Faktor $1/2$ berücksichtigt wieder, dass jeweils ein Symbol zwei Binärzeichen (Bit) beinhaltet.

(4)  Die Bitfehlerwahrscheinlichkeit ist nach der Lösung zur Teilaufgabe (2) gleich der Wahrscheinlichkeit, dass die beiden Rauschkomponenten gewisse Grenzen überschreiten:

$$p_{\rm B} = {\rm Pr}( n_1 < -\sqrt{E}) = {\rm Pr}( n_2 < -\sqrt{E}) \hspace{0.05cm}.$$

Beim AWGN–Kanal lautet diese Wahrscheinlichkeit mit der Varianz $\sigma_n^2 = N_0/2$:

$$p_{\rm B} = {\rm Q} \left ( { { \sqrt{E}}/{ \sigma_n} }\right ) = {\rm Q} \left ( \sqrt{ { {2E}}/{ N_0} }\right ) \hspace{0.05cm}.$$

Die mittlere Energie pro Symbol kann am einfachsten durch Mittelung über die quadratischen Abstände der Signalraumpunkte vom Ursprung bestimmt werden und ergibt $E_{\rm S} = 2E$. Die mittlere Energie pro Bit ist halb so groß: $E_{\rm B} = E_{\rm S}/2 = E$. Daraus folgt:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$

Richtig ist also der zweite Lösungsvorschlag. Zum gleichen Ergebnis kommt man auch, wenn man die 4–QAM wie im Kapitel Struktur des optimalen Empfängers des Buches „Modulationsverfahren” als zwei orthogonale (das heißt: sich nicht störende) BPSK–Systeme über den gleichen Kanal betrachtet.