Aufgaben:Exercise 5.2: Error Correlation Function

• Return to book

Gegebene Fehlerabstandswahrscheinlichkeiten und Fehlerkorrelationsfunktion

Zur Charakterisierung von digitalen Kanalmodellen verwendet man unter Anderem

• die Fehlerkorrelationsfunktion (FKF)

$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$

• die Fehlerabstandswahrscheinlichkeiten

$${\rm Pr}( a =k) \hspace{0.05cm}, \hspace{0.2cm} k \ge 1\hspace{0.05cm}.$$

Hierbei bezeichnen

• $〈e_{\rm \nu}〉$ die Fehlerfolge mit $e_{\rm \nu} ∈ \{0, 1\}$, und
• $a$ den Fehlerabstand.

Zwei direkt aufeinanderfolgende Bitfehler werden somit durch den Fehlerabstand $a = 1$ gekennzeichnet.

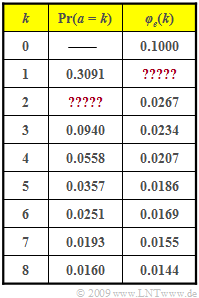
Die Tabelle zeigt beispielhafte Werte der Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a = k)$ sowie der Fehlerkorrelationsfunktion $\varphi_e(k)$. Einige Angaben fehlen in der Tabelle. Diese Werte sollen aus den gegebenen Werten berechnet werden.

Hinweise:

• Die Aufgabe behandel den Lehrstoff des Kapitels Beschreibungsgrößen digitaler Kanalmodelle.

Fragebogen

1

Welcher Wert ergibt sich für die mittlere Fehlerwahrscheinlichkeit?

$p_{\rm M} \ = \ $

2

Welcher Wert ergibt sich für den mittleren Fehlerabstand?

${\rm E}[a] \ = \ $

3

Berechnen Sie den FKF–Wert für $k = 1$.

$\varphi_r(k = 1) \ = \ $

4

Welche Näherung gilt für die Wahrscheinlichkeit des Fehlerabstands $a = 2$?

${\rm Pr}(a = 2) \ = \ $

Musterlösung

Solution

(1)  Die mittlere Fehlerwahrscheinlichkeit ist gleich dem FKF–Wert für $k = 0$. Wegen $e_{\nu} ∈ \{0, 1\}$ gilt nämlich:

$$\varphi_{e}(k = 0) = {\rm E}[e_{\nu}^2 ]= {\rm E}[e_{\nu} ]= p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm M}\hspace{0.15cm}\underline { = 0.1} \hspace{0.05cm}.$$

(2)  Der mittlere Fehlerabstand ist gleich dem Kehrwert der mittleren Fehlerwahrscheinlichkeit. Das heißt: $E[a] = 1/p_{\rm M} \ \underline {= 10}$.

(3)  Nach der Definitionsgleichung und dem Satz von Bayes erhält man folgendes Ergebnis:

$$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}] = {\rm E}[(e_{\nu} = 1) \cdot (e_{\nu + 1}=1)]=$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(e_{\nu + 1}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot {\rm Pr}(e_{\nu} = 1) \hspace{0.05cm}.$$

Die erste Wahrscheinlichkeits ist gleich ${\rm Pr}(a = 1)$ und die zweite Wahrscheinlichkeit ist gleich $p_{\rm M}$:

$$\varphi_{e}(k = 1) = 0.3091 \cdot 0.1\hspace{0.15cm}\underline { = 0.0309} \hspace{0.05cm}.$$

(4)  Der FKF–Wert $\varphi_e(k = 2)$ kann (näherungsweise) folgendermaßen interpretiert werden:

$$\varphi_{e}(k = 2) ={\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot p_{\rm M}$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = \frac{\varphi_{e}(k = 2)}{p_{\rm M}} = \frac{0.0267}{0.1} = 0.267\hspace{0.05cm}.$$

Diese Wahrscheinlichkeit setzt sich zusammen aus den beiden Möglichkeiten „Zum Zeitpunkt $\nu+1$ tritt tritt ein Fehler auf” sowie „Zum Zeitpunkt $\nu+1$ gibt es keinen Fehler”:

$${\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = {\rm Pr}( a =1) \cdot {\rm Pr}( a =1) + {\rm Pr}( a =2)$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr}( a =2)= 0.267 - 0.3091^2 \hspace{0.15cm}\underline {= 0.1715}\hspace{0.05cm}.$$

Bei der Rechnung wurde davon ausgegangen, dass die einzelnen Fehlerabstände statistisch voneinander unabhängig sind. Diese Annahme gilt allergings nur für eine besondere Klasse von Kanalmodellen, die man als „erneuernd” bezeichnet. Das hier betrachtete Bündelfehlermodell erfüllt diese Bedingung nicht. Die tatsächliche Wahrscheinlichkeit ${\rm Pr}(a = 2) = 0.1675$ weicht deshalb vom hier berechneten Wert ($0.1715$) geringfügig ab.