Difference between revisions of "Aufgaben:Exercise 4.10: Union Bound"
m (Hussain verschob die Seite A4.10 Union Bound nach 4.10 Union Bound) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
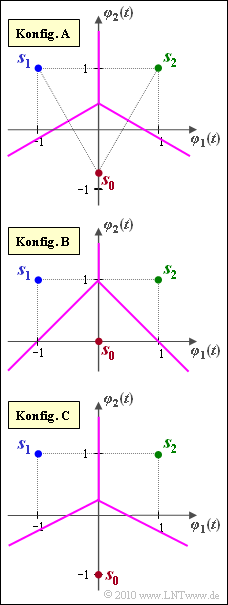
| − | [[File: | + | [[File:P_ID2043__Dig_A_4_10.png|right|frame|Signalraumkonstellationen mit <i>N</i> = 2, <i>M</i> = 3]] |
| + | Die so genannte „Union Bound” gibt eine obere Schranke für die Fehlerwahrscheinlichkeit eines nichtbinären Übertragungssystems ($M > 2$) an. Die tatsächliche (mittlere) Fehlerwahrscheinlichkeit ist allgemein wie folgt gegeben: | ||
| + | :$${\rm Pr}({ \cal E}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum\limits_{i = 0 }^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.05cm},$$ | ||
| + | :$$ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \rm wobei}$$ | ||
| + | :$${ \cal E}_{ik}: \boldsymbol{ r }{\rm \hspace{0.15cm}liegt \hspace{0.15cm}n\ddot{a}her \hspace{0.15cm}bei \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}als \hspace{0.15cm}beim \hspace{0.15cm}Sollwert \hspace{0.15cm}}\boldsymbol{ s }_i | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die einfachere Union Bound liefert eine obere Schranke für die Verfälschungswahrscheinlichkeit unter der Voraussetzung, dass die Nachricht $m_i$ (bzw. das Signal $\boldsymbol{s}_i$) gesendet wurde: | ||
| + | :$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ \ge \ \hspace{-0.1cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s }_i ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i )\hspace{0.05cm},\$$ | ||
| + | :$$ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ = \ \hspace{-0.2cm}\sum\limits_{k = 0 ,\hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm} | ||
| + | {\rm Pr}({ \cal E}_{ik}) = \hspace{-0.1cm}\sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm}{\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right )\hspace{0.05cm}. $$ | ||
| + | |||
| + | Dabei sind folgende Abkürzungen verwendet: | ||
| + | * ${\rm Q}(x)$ ist die komplementäre Gaußsche Fehlerfunktion, | ||
| + | * $d_{ik}$ bezeichnet den Abstand der Signalpunkte $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$, | ||
| + | * $\sigma_n$ gibt der Effektivwert (⇒ Wurzel aus der Varianz) des additiven weißen Gaußschen Rauschens an. | ||
| + | |||
| + | |||
| + | Durch Mittelung über alle möglichen Signale $\boldsymbol{s}_i$ kommt man dann zur eigentlichen Union Bound: | ||
| + | :$$p_{{\rm UB}} = \sum\limits_{i = 0 }^{M-1} {\rm Pr}(\boldsymbol{ s }_i) \cdot p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \ge {\rm Pr}({ \cal E}) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Grafik zeigt drei verschiedene Signalraumkonstellationen mit jeweils $M = 3$ Signalpunkten $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ im zweidimensionalen Raum ($N = 2$). Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sind geeignet normiert. Somit sind auch die Signalraumkoordinaten reine Zahlenwerte ohne Einheit: | ||
| + | :$$\boldsymbol{ s }_1 = (-1, \hspace{0.1cm}+1)\hspace{0.05cm}, \hspace{0.2cm} | ||
| + | \boldsymbol{ s }_2 = (+1, \hspace{0.1cm}+1)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Der Signalraumpunkt $\boldsymbol{s}_0$ in der Konfiguration $A$ liegt so, dass $\boldsymbol{s}_0$, $\boldsymbol{s}_1$, $\boldsymbol{s}_2$ ein gleichseitiges Dreieck beschreiben. Bei der Konfiguration $B$ und $C$ gilt dagegen $\boldsymbol{s}_0 = (0, 0)$ bzw. $\boldsymbol{s}_0 = (0, \ –1)$. Verwenden Sie für alle Berechnungen den AWGN–Effektivwert $\sigma_n = 0.5$. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. | ||
| + | * Gegeben sind folgende Werte der komplementären Gaußschen Fehlerfunktion: | ||
| + | :$${\rm Q}(1) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.159\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(\sqrt{2}) \approx 0.079\hspace{0.05cm}, \hspace{0.23cm}{\rm Q}(\sqrt{3}) \approx 0.042\hspace{0.05cm},$$ | ||
| + | :$${\rm Q}(2) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.023\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.14) \approx 0.016\hspace{0.05cm}, \hspace{0.1cm}{\rm Q}(\sqrt{5}) \approx 0.013 \hspace{0.05cm}.$$ | ||
Revision as of 17:37, 16 November 2017
Die so genannte „Union Bound” gibt eine obere Schranke für die Fehlerwahrscheinlichkeit eines nichtbinären Übertragungssystems ($M > 2$) an. Die tatsächliche (mittlere) Fehlerwahrscheinlichkeit ist allgemein wie folgt gegeben:
- $${\rm Pr}({ \cal E}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum\limits_{i = 0 }^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.05cm},$$
- $$ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \rm wobei}$$
- $${ \cal E}_{ik}: \boldsymbol{ r }{\rm \hspace{0.15cm}liegt \hspace{0.15cm}n\ddot{a}her \hspace{0.15cm}bei \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}als \hspace{0.15cm}beim \hspace{0.15cm}Sollwert \hspace{0.15cm}}\boldsymbol{ s }_i \hspace{0.05cm}.$$
Die einfachere Union Bound liefert eine obere Schranke für die Verfälschungswahrscheinlichkeit unter der Voraussetzung, dass die Nachricht $m_i$ (bzw. das Signal $\boldsymbol{s}_i$) gesendet wurde:
- $$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ \ge \ \hspace{-0.1cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s }_i ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i )\hspace{0.05cm},\$$
- $$ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ = \ \hspace{-0.2cm}\sum\limits_{k = 0 ,\hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm} {\rm Pr}({ \cal E}_{ik}) = \hspace{-0.1cm}\sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm}{\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right )\hspace{0.05cm}. $$
Dabei sind folgende Abkürzungen verwendet:
- ${\rm Q}(x)$ ist die komplementäre Gaußsche Fehlerfunktion,
- $d_{ik}$ bezeichnet den Abstand der Signalpunkte $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$,
- $\sigma_n$ gibt der Effektivwert (⇒ Wurzel aus der Varianz) des additiven weißen Gaußschen Rauschens an.
Durch Mittelung über alle möglichen Signale $\boldsymbol{s}_i$ kommt man dann zur eigentlichen Union Bound:
- $$p_[[:Template:\rm UB]] = \sum\limits_{i = 0 }^{M-1} {\rm Pr}(\boldsymbol{ s }_i) \cdot p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \ge {\rm Pr}({ \cal E}) \hspace{0.05cm}.$$
Die Grafik zeigt drei verschiedene Signalraumkonstellationen mit jeweils $M = 3$ Signalpunkten $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ im zweidimensionalen Raum ($N = 2$). Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sind geeignet normiert. Somit sind auch die Signalraumkoordinaten reine Zahlenwerte ohne Einheit:
- $$\boldsymbol{ s }_1 = (-1, \hspace{0.1cm}+1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (+1, \hspace{0.1cm}+1)\hspace{0.05cm}.$$
Der Signalraumpunkt $\boldsymbol{s}_0$ in der Konfiguration $A$ liegt so, dass $\boldsymbol{s}_0$, $\boldsymbol{s}_1$, $\boldsymbol{s}_2$ ein gleichseitiges Dreieck beschreiben. Bei der Konfiguration $B$ und $C$ gilt dagegen $\boldsymbol{s}_0 = (0, 0)$ bzw. $\boldsymbol{s}_0 = (0, \ –1)$. Verwenden Sie für alle Berechnungen den AWGN–Effektivwert $\sigma_n = 0.5$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Approximation der Fehlerwahrscheinlichkeit.
- Gegeben sind folgende Werte der komplementären Gaußschen Fehlerfunktion:
- $${\rm Q}(1) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.159\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(\sqrt{2}) \approx 0.079\hspace{0.05cm}, \hspace{0.23cm}{\rm Q}(\sqrt{3}) \approx 0.042\hspace{0.05cm},$$
- $${\rm Q}(2) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.023\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.14) \approx 0.016\hspace{0.05cm}, \hspace{0.1cm}{\rm Q}(\sqrt{5}) \approx 0.013 \hspace{0.05cm}.$$
Fragebogen
Musterlösung