Aufgaben:Exercise 2.4: Dual Code and Gray Code

• Return to book

Quaternärsignale mit Dual- und Graycodierung

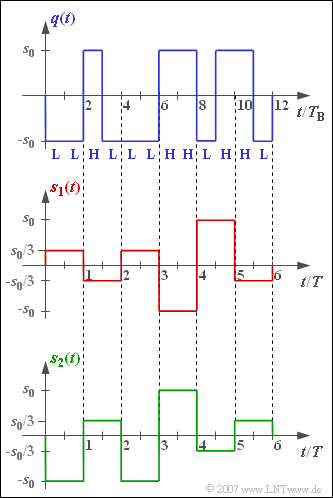
Die beiden dargestellten Signale $s_{1}(t)$ und $s_{2}(t)$ sind zwei unterschiedliche Realisierungen eines redundanzfreien quaternären Sendesignals, die beide vom blau gezeichneten Quellensignal $q(t)$ abgeleitet wurden. Bei einem der Sendesignale wurde der sog. $\color{red} {\rm Dualcode}$ mit der Zuordnung

$$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.15cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,$$

$$\mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.15cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$

verwendet, beim anderen eine bestimmte Form eines $\color{red} {\rm Graycodes}$. Dieser zeichnet sich dadurch aus, dass sich die Binärdarstellung benachbarter Amplitudenwerte immer nur in einem einzigen Bit unterscheiden.

Bei der Lösung der Aufgabe soll von folgenden Voraussetzungen ausgegangen werden:

• Die Amplitudenstufen liegen bei $±3\ \rm V$ und $±1 \ \rm V$. Die Entscheiderschwellen liegen in der Mitte zwischen zwei benachbarten Amplitudenwerten, also bei $–2\ \rm V$, $0\ \rm V$ und $+2\ \rm V$.
• Der Rauscheffektivwert ist $\sigma_{d}$. Dieser ist so zu wählen, dass die Verfälschungswahrscheinlichkeit vom äußeren Symbol $(+s_0)$ zum nächstgelegenen Symbol $(+s_{0}/3)$ genau $p = 1\%$ beträgt.
• Verfälschungen zu nicht benachbarten Symbolen können ausgeschlossen werden; bei Gaußschen Störungen ist diese Vereinfachung in der Praxis stets erlaubt.
• Man unterscheidet grundsätzlich zwischen der $\color{red} {\rm Symbolfehlerwahrscheinlichkeit} \ p_{\rm S}$ (bezogen auf das Quaternärsignal) und der $\color{red} {\rm Bitfehlerwahrscheinlichkeit} \ p_{B}$ (bezogen auf das Quellensignal).

Hinweise:

• Die Aufgabe gehört zum Kapitel Grundlagen der codierten Übertragung.
• Bezug genommen wird auch auf das Kapitel Redundanzfreie Codierung .
• Berücksichtigen Sie, dass Autokorrelationsfunktion (AKF) und Leistungsdichtespektrum (LDS) eines stochastischen Signals stets über die Fouriertransformation zusammenhängen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Hinweis:

Die Aufgabe gehört zum Themengebiet von Redundanzfreie Codierung. Zur numerischen Auswertung der Q–Funktion können Sie das folgende Interaktionsmodul benutzen:

Komplementäre Gaußsche Fehlerfunktionen

Fragebogen

1

Welches der Signale $s_{1}(t)$ bzw. $s_{2}(t)$ verwendet eine Graycodierung?

	$s_{1}(t)$ verwendet eine Graycodierung.
	$s_{2}(t)$ verwendet eine Graycodierung.

2

Bestimmen Sie den Rauscheffektivwert aus der angegebenen Bedingung.

$\sigma_{d} \ = \ $ $\ \rm V$

3

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit dem Graycode?

$p_{\rm S} \ = \ $ $\ \%$

4

Welche Bitfehlerwahrscheinlichkeit ergibt sich mit dem Graycode?

$p_{\rm B} \ = \ $ $\ \%$

5

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit dem Dualcode?

$p_{\rm S} \ = \ $ $\ \%$

6

Welche Bitfehlerwahrscheinlichkeit ergibt sich mit dem Dualcode?

$p_{\rm B} \ = \ $ $\ \%$

Musterlösung

Solution

(1)  Im Signal $s_{2}(t)$ erkennt man die Realisierung des vorne angegebenen Dualcodes. Dagegen wurde beim Signal $s_{2}(t)$ ein Graycode $\Rightarrow$ Lösungsvorschlag 1 mit folgender Zuordnung verwendet:

$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.15cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.15cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.15cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$

(2)  Die Wahrscheinlichkeit $p$, dass der Amplitudenwert $3 \rm V$ aufgrund des gaußverteilten Rauschens mit der Streuung $\sigma_{d}$ die benachbarte Entscheiderschwelle $2 \rm V$ unterschreitet, soll $1 \%$ betragen. Daraus folgt:

$$p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$

(3)  Die beiden äußeren Symbole werden jeweils mit der Wahrscheinlichkeit $p$ verfälscht, die beiden inneren mit der doppelten Wahrscheinlichkeit $(2p)$. Durch Mittelung unter Berücksichtigung gleicher Symbolauftrittswahrscheinlichkeiten erhält man

$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$

(4)  Jeder Symbolfehler führt genau zu einem Bitfehler. Da jedoch jedes Quaternärsymbol genau zwei Binärsymbole beinhaltet, ergibt sich für die Bitfehlerwahrscheinlichkeit:

$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$

(5)  Bei der Berechnung der Symbolfehlerwahrscheinlichkeit pS wird das verwendete Mapping nicht berücksichtigt. Wie in der Teilaufgabe c) erhält man somit $p_{\rm S} \underline{ = 1.5 \%}$.

(6)  Die beiden äußeren Symbole werden mit $p$ verfälscht und führen auch beim Dualcode jeweils nur zu einem Bitfehler. Die inneren Symbole werden mit $2p$ verfälscht und führen nun im Mittel zu $1.5$ Bitfehlern. Unter Berücksichtigung des Faktors $2$ im Nenner – siehe Teilaufgabe (2) – erhält man somit für die Bitfehlerwahrscheinlichkeit des Dualcodes:

$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$