Difference between revisions of "Aufgaben:Exercise 4.08Z: Error Probability with Three Symbols"
m (Guenter verschob die Seite 4.8Z Fehlerwahrscheinlichkeit nach 4.08Z Fehlerwahrscheinlichkeit) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
| − | [[File:P_ID2037__Dig_Z_4_8.png|right|frame|Entscheidungsregionen | + | [[File:P_ID2037__Dig_Z_4_8.png|right|frame|Entscheidungsregionen bei <i>M</i> = 3 Symbolen]] |
| − | Die Grafik zeigt die genau gleiche Signalraumkonstellation wie in der [[Aufgaben:4.8_Entscheidungsregionen| Aufgabe | + | Die Grafik zeigt die genau gleiche Signalraumkonstellation wie in der [[Aufgaben:4.8_Entscheidungsregionen| Aufgabe 4.8]]: |
* die $M = 3$ möglichen Sendesignale, nämlich | * die $M = 3$ möglichen Sendesignale, nämlich | ||
:$$\boldsymbol{ s }_0 = (-1, \hspace{0.1cm}1)\hspace{0.05cm}, \hspace{0.2cm} | :$$\boldsymbol{ s }_0 = (-1, \hspace{0.1cm}1)\hspace{0.05cm}, \hspace{0.2cm} | ||
| Line 10: | Line 10: | ||
* die $M = 3$ Entscheidungsgrenzen | * die $M = 3$ Entscheidungsgrenzen | ||
| − | :$$G_{01}: y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1.5 - 2 \cdot x\hspace{0.05cm},$$ | + | :$$G_{01}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1.5 - 2 \cdot x\hspace{0.05cm},$$ |
| − | :$$ | + | :$$G_{02}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.75 +1.5 \cdot x\hspace{0.05cm},$$ |
| − | :$$ | + | :$$G_{12}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} x/3\hspace{0.05cm}.$$ |
| Line 31: | Line 31: | ||
Ein solches amplitudenbegrenztes Rauschen ist zwar ohne jede praktische Bedeutung. Es ermöglicht jedoch eine Fehlerwahrscheinlichkeitsberechnung ohne umfangreiche Integrale, aus der das Prinzip der Vorgehensweise erkennbar wird. | Ein solches amplitudenbegrenztes Rauschen ist zwar ohne jede praktische Bedeutung. Es ermöglicht jedoch eine Fehlerwahrscheinlichkeitsberechnung ohne umfangreiche Integrale, aus der das Prinzip der Vorgehensweise erkennbar wird. | ||
| − | '' | + | |
| − | * Die Aufgabe gehört zum | + | |
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | * Zur Vereinfachung der Schreibweise wird nachfolgend verwendet: | ||
| + | :$$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} | ||
| + | y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$ | ||
| Line 40: | Line 46: | ||
{Welchen Wert besitzt die Konstante $K$ für $A = 0.75$? | {Welchen Wert besitzt die Konstante $K$ für $A = 0.75$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\boldsymbol{K}$ | + | $\boldsymbol{K} \ = \ $ { 0.444 3% } |
{Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit $A = 0.75$? | {Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit $A = 0.75$? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_{\rm S} \ = \ $ { 0. } |
{Welche Aussagen sind für $A = 1$ zutreffend? | {Welche Aussagen sind für $A = 1$ zutreffend? | ||
|type="[]"} | |type="[]"} | ||
- Alle Nachrichten $m_i$ werden in gleicher Weise verfälscht. | - Alle Nachrichten $m_i$ werden in gleicher Weise verfälscht. | ||
| − | + Die bedingte Fehlerwahrscheinlichkeit ${\rm Pr(Fehler \ | \ \it | + | + Die bedingte Fehlerwahrscheinlichkeit ${\rm Pr(Fehler} \hspace{0.05cm} | \hspace{0.05cm} {\it m}_0) = 1/64$. |
| − | - Die bedingte Fehlerwahrscheinlichkeit ${\rm Pr(Fehler \ | \ \it | + | - Die bedingte Fehlerwahrscheinlichkeit ${\rm Pr(Fehler} \hspace{0.05cm} | \hspace{0.05cm} {\it m}_1) = 0$. |
| − | + Die bedingte Fehlerwahrscheinlichkeit ${\rm Pr(Fehler \ | \ \it | + | + Die bedingte Fehlerwahrscheinlichkeit ${\rm Pr(Fehler} \hspace{0.05cm} | \hspace{0.05cm} {\it m}_2) = 0$. |
| − | {Welche Fehlerwahrscheinlichkeit ergibt sich mit ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) = 1/3$? | + | {Welche Fehlerwahrscheinlichkeit ergibt sich mit $A=1$ und ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) = 1/3$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_{\rm S} \ = \ $ { 1.04 3% } $\ \%$ |
| − | {Welche Fehlerwahrscheinlichkeit ergibt sich mit ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 1/4, {\rm Pr}(m_2) = 1/2$? | + | {Welche Fehlerwahrscheinlichkeit ergibt sich mit $A=1$ und ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 1/4, {\rm Pr}(m_2) = 1/2$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_{\rm S} \ = \ $ { 0.78 3% } $\ \%$ |
{Könnte man durch Festlegung anderer Regionen ein besseres Ergebnis erzielen? | {Könnte man durch Festlegung anderer Regionen ein besseres Ergebnis erzielen? | ||
|type="()"} | |type="()"} | ||
| − | + | + | + Ja. |
| − | - | + | - Nein. |
</quiz> | </quiz> | ||
Revision as of 16:27, 20 November 2017
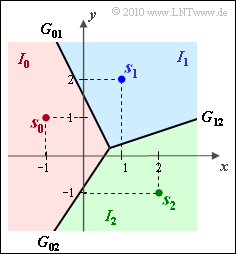
Die Grafik zeigt die genau gleiche Signalraumkonstellation wie in der Aufgabe 4.8:
- die $M = 3$ möglichen Sendesignale, nämlich
- $$\boldsymbol{ s }_0 = (-1, \hspace{0.1cm}1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 = (1, \hspace{0.1cm}2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (2, \hspace{0.1cm}-1)\hspace{0.05cm}.$$
- die $M = 3$ Entscheidungsgrenzen
- $$G_{01}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1.5 - 2 \cdot x\hspace{0.05cm},$$
- $$G_{02}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.75 +1.5 \cdot x\hspace{0.05cm},$$
- $$G_{12}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} x/3\hspace{0.05cm}.$$
Die beiden Achsen des 2D–Signalraums sind hier vereinfachend mit $x$ und $y$ bezeichnet; eigentlich müsste hierfür $\varphi_1(t)/\sqrt {E}$ bzw. $\varphi_2(t)/\sqrt {E}$ geschrieben werden.
Diese Entscheidungsgrenzen sind optimal unter den Voraussetzungen
- gleichwahrscheinliche Symbolwahrscheinlichkeiten
- zirkulär–symmetrische WDF des Rauschens (z.B. AWGN).
In dieser Aufgabe betrachten wir dagegen für die Rausch–WDF eine zweidimensionale Gleichverteilung:
- $$\boldsymbol{ p }_{\boldsymbol{ n }} (x,\hspace{0.15cm} y) = \left\{ \begin{array}{c} K\\ 0 \end{array} \right.\quad \begin{array}{*{1}c}{\rm f\ddot{u}r} \hspace{0.15cm}|x| <A, \hspace{0.15cm} |y| <A \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}.\\ \end{array}$$
Ein solches amplitudenbegrenztes Rauschen ist zwar ohne jede praktische Bedeutung. Es ermöglicht jedoch eine Fehlerwahrscheinlichkeitsberechnung ohne umfangreiche Integrale, aus der das Prinzip der Vorgehensweise erkennbar wird.
Hinweise:
- Die Aufgabe gehört zum Kapitel Approximation der Fehlerwahrscheinlichkeit.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Zur Vereinfachung der Schreibweise wird nachfolgend verwendet:
- $$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$2A \cdot 2A \cdot K = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = \frac{1}{4A^2}\hspace{0.05cm}.$$
Mit $A = 0.75$ ⇒ $2A = 3/2$ erhält man $K = 4/9 = \ \underline {0.444}$.
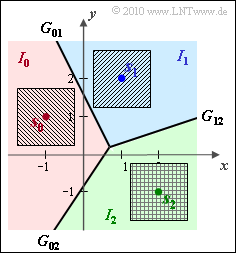
(3) Richtig sind die Aussagen 2 und 4, wie aus der unteren Grafik abgelesen werden kann.
- Die Nachricht $m_2$ kann nicht verfälscht werden, da das Quadrat um $\boldsymbol{s}_2$ vollständig im rechten unteren Quadranten und damit im Entscheidungsgebiet $I_2$ liegt.
- Ebenso wurde mit Sicherheit $m_2$ gesendet, wenn der Empfangswert im Entscheidungsgebiet $I_2$ liegt. Der Grund: Keines der Quadrate um $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ reicht bis in das Gebiet $I_2$ hinein.
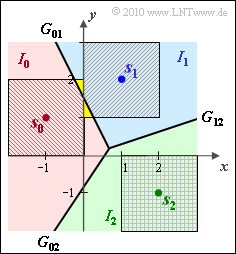
- $m_0$ kann nur zu $m_1$ verfälscht werden. Die (bedingte) Verfälschungswahrscheinlichkeit ist gleich dem Verhältnis der Flächen des gelben Dreiecks (Fläche $1/16$) und des Quadrats (Fläche 4):
- $${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) = \frac{1/2 \cdot 1/2 \cdot 1/4}{4}= {1}/{64} \hspace{0.05cm}.$$
- Aus Symmetriegründen gilt gleichermaßen:
- $${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 )={1}/{64} \hspace{0.05cm}. $$
(4) Bei gleichwahrscheinlichen Symbolen erhält man für die (mittlere) Fehlerwahrscheinlichkeit:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{3} \cdot \left [{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) + {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 )+{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_2 )\right ]=$$
- $$ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{3} \cdot \left [{1}/{64} + {1}/{64} + 0 )\right ]= \frac{2}{3 \cdot 64} = {1}/{96}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.0104} \hspace{0.05cm}.$$
(5) Nun ergibt sich eine kleinere mittlere Fehlerwahrscheinlichkeit, nämlich
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {1}/{4} \cdot {1}/{64} + {1}/{4} \cdot {1}/{64}+ {1}/{2} \cdot0 = {1}/{128}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.0078 } \hspace{0.05cm}. $$
(6) Richtig ist JA. Beispielsweise ergäbe sich durch $I_1$: erster Quadrant, $I_0$: zweiter Quadrant, $I_2 \text{:} \ y < 0$ die Fehlerwahrscheinlichkeit $0$. Das bedeutet, dass die vorgegebenen Grenzen nur bei zirkulär symmetrischer WDF des Rauschens optimal sind, zum Beispiel beim AWGN–Kanal.