Difference between revisions of "Aufgaben:Exercise 3.1: Analysis of a Convolutional Encoder"
From LNTwww
| Line 22: | Line 22: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die | + | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Grundlagen_der_Faltungscodierung| Grundlagen der Faltungscodierung]]. |
| + | * Der Vollständigkeit halber werden hier auch die Codebits zum Taktschritt $i = 2$ angegeben: | ||
| + | :$$x_2^{(1)} = 1 \hspace{0.05cm},\hspace{0.4cm}x_2^{(2)} = 0 \hspace{0.05cm},\hspace{0.4cm} | ||
| + | x_2^{(3)} = 0 ,\hspace{0.4cm}x_2^{(4)} = 0 \hspace{0.05cm}.$$ | ||
| + | |||
| + | # Diese letzte Angabe wird zur Lösung der Aufgabe allerdings nicht benötigt. | ||
| + | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
Revision as of 09:07, 22 November 2017
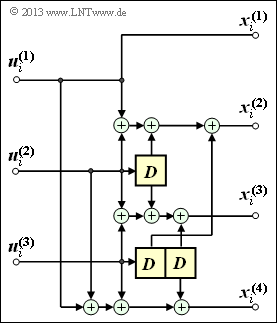
Wir betrachten den nebenstehenden Faltungscodierer und gehen von folgender Informationssequenz:
- $$\underline{\it u} = \big( 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm}... \big )\hspace{0.05cm}.$$
Diese Sequenz wird auf drei Stränge aufgeteilt:
- $$\underline{\it u}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} ... \big )\hspace{0.05cm},$$
- $$\underline{\it u}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} ... \big )\hspace{0.05cm},$$
- $$\underline{\it u}^{(3)} \hspace{-0.15cm} \ = \hspace{-0.15cm} \big( 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} ... \big )\hspace{0.05cm}.$$
Die zum Zeitpunkt $i$ am Coder anliegenden Bits werden mit $u_i^{\rm (1)}$, $u_i^{\rm (2)}$ und $u_i^{\rm (3)}$ bezeichnet. Beispielsweise gilt $u_1^{\rm (1)} = 0$, $u_2^{\rm (2)} = 1$ sowie $u_3^{\rm (3)} = 1$.
In dieser Aufgabe sollen ermittelt werden:
- die Anzahl $k$ der pro Codierschritt verarbeiteten Informationsbits,
- die Anzahl $n$ der pro Codierschritt ausgegebenen Codebits,
- die Gedächtnisordnung (oder kurz: das Gedächtnis) $m$,
- die Gesamteinflusslänge (oder kurz: Einflusslänge) $\nu$.
Außerdem sollen Sie für die angegebene Informationssequenz $\underline {u}$ die Codesymbole $x_i^{(1)}$, $x_i^{(2)}$, $x_i^{(3)}$, $x_i^{(4)}$ für die Taktzeitpunkte $i = 1$ und $i = 3$ bestimmen. Dabei ist vorauszusetzen, dass alle Speicherelemente zu Beginn mit Nullen belegt waren.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Grundlagen der Faltungscodierung.
- Der Vollständigkeit halber werden hier auch die Codebits zum Taktschritt $i = 2$ angegeben:
- $$x_2^{(1)} = 1 \hspace{0.05cm},\hspace{0.4cm}x_2^{(2)} = 0 \hspace{0.05cm},\hspace{0.4cm} x_2^{(3)} = 0 ,\hspace{0.4cm}x_2^{(4)} = 0 \hspace{0.05cm}.$$
- Diese letzte Angabe wird zur Lösung der Aufgabe allerdings nicht benötigt.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)