Difference between revisions of "Aufgaben:Exercise 1.2: A Simple Binary Channel Code"
From LNTwww
| Line 4: | Line 4: | ||
[[File:P_ID2381__KC_A_1_2.png|right|frame|Zur Verdeutlichung der Kanalcodierung]] | [[File:P_ID2381__KC_A_1_2.png|right|frame|Zur Verdeutlichung der Kanalcodierung]] | ||
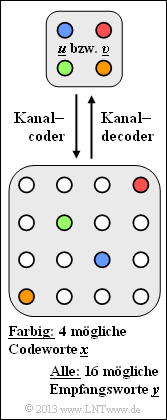
Die Grafik verdeutlicht die hier betrachtete Kanalcodierung C: | Die Grafik verdeutlicht die hier betrachtete Kanalcodierung C: | ||
| − | *Es gibt vier mögliche Informationsblöcke u = ( | + | *Es gibt vier mögliche Informationsblöcke $\underline{u} = (u_{1}, u_{2}, ... , u_{k})$. |
| − | *Jeder Informationsblock u wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort x = ( | + | *Jeder Informationsblock u wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort $\underline{x}= (x_{1}, x_{2}, ... , x_{n})$ zugeordnet. |
| − | *Aufgrund von Decodierfehlern (0 → 1, 1 → 0) gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte y = ( | + | *Aufgrund von Decodierfehlern (0 → 1, 1 → 0) gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte $\underline{y} = (y_{1}, y_{2}, ... , y_{n})$. |
Ab Teilaufgabe d) betrachten wir folgende Zuordnung: | Ab Teilaufgabe d) betrachten wir folgende Zuordnung: | ||
| + | :$$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},$$ | ||
| + | :$$\underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$ | ||
| + | :$$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},$$ | ||
| + | :$$\underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$ | ||
''Hinweis:'' | ''Hinweis:'' | ||
| Line 14: | Line 18: | ||
*Hamming–Gewicht, | *Hamming–Gewicht, | ||
*Hamming–Distanz, usw. | *Hamming–Distanz, usw. | ||
| − | werden auf | + | werden auf [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Blockschaltbild_und_Voraussetzungen|Blockschaltbild_und_Voraussetzungen]] und [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung|Einige_wichtige_Definitionen_zur_Blockcodierung]] von Kanalcodierung definiert. |
Revision as of 13:05, 22 November 2017
Die Grafik verdeutlicht die hier betrachtete Kanalcodierung C:
- Es gibt vier mögliche Informationsblöcke $\underline{u} = (u_{1}, u_{2}, ... , u_{k})$.
- Jeder Informationsblock u wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort $\underline{x}= (x_{1}, x_{2}, ... , x_{n})$ zugeordnet.
- Aufgrund von Decodierfehlern (0 → 1, 1 → 0) gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte $\underline{y} = (y_{1}, y_{2}, ... , y_{n})$.
Ab Teilaufgabe d) betrachten wir folgende Zuordnung:
- $$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},$$
- $$\underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$
- $$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},$$
- $$\underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$
Hinweis:
Die hier abgefragten Beschreibungsgrößen wie
- Coderate,
- Hamming–Gewicht,
- Hamming–Distanz, usw.
werden auf Blockschaltbild_und_Voraussetzungen und Einige_wichtige_Definitionen_zur_Blockcodierung von Kanalcodierung definiert.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.