Difference between revisions of "Channel Coding/The Basics of Product Codes"
| Line 8: | Line 8: | ||
== Grundstruktur eines Produktcodes == | == Grundstruktur eines Produktcodes == | ||
<br> | <br> | ||
| − | Die Grafik zeigt den prinzipiellen Aufbau von Produktcodes, die bereits 1954 von Peter Elias eingeführt wurden. Der nachfolgend dargestellte <span style="font-weight: bold;">zweidimensionale Produktcode</span> | + | Die Grafik zeigt den prinzipiellen Aufbau von Produktcodes, die bereits 1954 von Peter Elias eingeführt wurden. Der nachfolgend dargestellte <span style="font-weight: bold;">zweidimensionale Produktcode</span> $C = C_1 × C_2$ basiert auf den beiden linearen und binären Blockcodes mit den Parametern $(n_1, \ k_1)$ bzw. $(n_2, \ k_2)$.<br> |
| − | [[File:P ID3000 KC T 4 2 S1 v1.png|Grundstruktur eines Produktcodes|class=fit]]<br> | + | [[File:P ID3000 KC T 4 2 S1 v1.png|center|frame|Grundstruktur eines Produktcodes|class=fit]]<br> |
| − | Die Codewortlänge ist | + | Die Codewortlänge ist $n = n_1 \cdot n_2$. Diese $n$ Codebits lassen sich wie folgt gruppieren: |
| − | *Die | + | *Die $k = k_1 \cdot k_2$ Informationsbits sind in der $k_2 × k_1$–Matrix $\mathbf{U}$ angeordnet. Die Coderate ist gleich dem Produkt der Coderaten der beiden Basiscodes: $R = k/n = (k_1/n_1) \cdot (k_2/n_2) = R_1 \cdot R_2$.<br> |
| − | *Die rechte obere Matrix | + | *Die rechte obere Matrix $\mathbf{P}^{(1)}$ mit der Dimension $k_2 × m_1$ beinhaltet die Prüfbits (englisch: <i>Parity</i>) hinsichtlich des Codes $C_1$. In jeder der $k_2$ Zeilen werden zu den $k_1$ Informationsbits $m_1 = n_1 \, –k_1$ Prüfbits hinzugefügt, wie in [[Kanalcodierung/Beispiele_bin%C3%A4rer_Blockcodes#Hamming.E2.80.93Codes_.282.29| Kapitel 1.3]] am Beispiel der Hamming–Codes beschrieben wurde.<br> |
| − | *Die linke untere Matrix | + | *Die linke untere Matrix $\mathbf{P}^{(2)}$ der Dimension $m_2 × k_1$ beinhaltet die Prüfbits hinsichtlich des zweiten Komponentencodes $C_2$. Hier erfolgt die Codierung (und auch die Decodierung) zeilenweise: In jeder der $k_1$ Spalten werden die $k_2$ Informationsbits noch um $m_2 = n_2 \, –k_2$ Prüfbits ergänzt.<br> |
| − | *Die | + | *Die $m_2 × m_1$–Matrix $\mathbf{P}^{(12)}$ rechts unten bezeichnet man als <i>Checks–on–Checks</i>. Hier werden die vorher erzeugten Parity–Matrizen $\mathbf{P}^{(1)}$ und $\mathbf{P}^{(2)}$ entsprechend den Prüfgleichungen verknüpft.<br><br> |
Alle Produktcodes entsprechend obiger Grafik weisen folgende <b>Eigenschaften</b> auf: | Alle Produktcodes entsprechend obiger Grafik weisen folgende <b>Eigenschaften</b> auf: | ||
| − | *Bei linearen Komponentencodes | + | *Bei linearen Komponentencodes $C_1$ und $C_2$ ist auch der Produktcode $C = C_1 × C_2$ linear.<br> |
| − | *Jede Zeile von | + | *Jede Zeile von $C$ gibt ein Codewort von $C_1$ wieder und jede Spalte ein Codewort von $C_2$.<br> |
| − | *Die Summe zweier Zeilen ergibt aufgrund der Linearität wieder ein Codewort von | + | *Die Summe zweier Zeilen ergibt aufgrund der Linearität wieder ein Codewort von $C_1$.<br> |
| − | *Ebenso ergibt die Summe zweier Spalten ein gültiges Codewort von | + | *Ebenso ergibt die Summe zweier Spalten ein gültiges Codewort von $C_2$.<br> |
| − | *Jeder Produktcodes beinhaltet auch das Nullwort | + | *Jeder Produktcodes beinhaltet auch das Nullwort $\underline{0}$ (ein Vektor mit $n$ Nullen).<br> |
| − | *Die minimale Distanz von | + | *Die minimale Distanz von $C$ ist $d_{\rm min} = d_1 \cdot d_2$, wobei $d_i$ die minimale Distanz von $C_i$ angibt.<br><br> |
== Iterative Syndromdecodierung von Produktcodes (1) == | == Iterative Syndromdecodierung von Produktcodes (1) == | ||
Revision as of 12:31, 28 November 2017
Contents
Grundstruktur eines Produktcodes
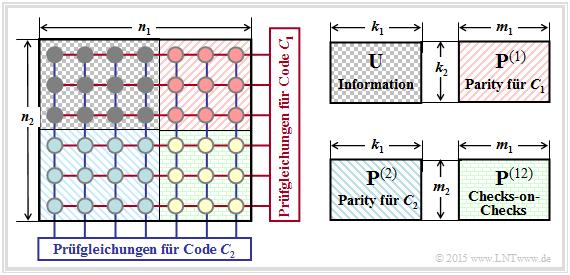
Die Grafik zeigt den prinzipiellen Aufbau von Produktcodes, die bereits 1954 von Peter Elias eingeführt wurden. Der nachfolgend dargestellte zweidimensionale Produktcode $C = C_1 × C_2$ basiert auf den beiden linearen und binären Blockcodes mit den Parametern $(n_1, \ k_1)$ bzw. $(n_2, \ k_2)$.
Die Codewortlänge ist $n = n_1 \cdot n_2$. Diese $n$ Codebits lassen sich wie folgt gruppieren:
- Die $k = k_1 \cdot k_2$ Informationsbits sind in der $k_2 × k_1$–Matrix $\mathbf{U}$ angeordnet. Die Coderate ist gleich dem Produkt der Coderaten der beiden Basiscodes: $R = k/n = (k_1/n_1) \cdot (k_2/n_2) = R_1 \cdot R_2$.
- Die rechte obere Matrix $\mathbf{P}^{(1)}$ mit der Dimension $k_2 × m_1$ beinhaltet die Prüfbits (englisch: Parity) hinsichtlich des Codes $C_1$. In jeder der $k_2$ Zeilen werden zu den $k_1$ Informationsbits $m_1 = n_1 \, –k_1$ Prüfbits hinzugefügt, wie in Kapitel 1.3 am Beispiel der Hamming–Codes beschrieben wurde.
- Die linke untere Matrix $\mathbf{P}^{(2)}$ der Dimension $m_2 × k_1$ beinhaltet die Prüfbits hinsichtlich des zweiten Komponentencodes $C_2$. Hier erfolgt die Codierung (und auch die Decodierung) zeilenweise: In jeder der $k_1$ Spalten werden die $k_2$ Informationsbits noch um $m_2 = n_2 \, –k_2$ Prüfbits ergänzt.
- Die $m_2 × m_1$–Matrix $\mathbf{P}^{(12)}$ rechts unten bezeichnet man als Checks–on–Checks. Hier werden die vorher erzeugten Parity–Matrizen $\mathbf{P}^{(1)}$ und $\mathbf{P}^{(2)}$ entsprechend den Prüfgleichungen verknüpft.
Alle Produktcodes entsprechend obiger Grafik weisen folgende Eigenschaften auf:
- Bei linearen Komponentencodes $C_1$ und $C_2$ ist auch der Produktcode $C = C_1 × C_2$ linear.
- Jede Zeile von $C$ gibt ein Codewort von $C_1$ wieder und jede Spalte ein Codewort von $C_2$.
- Die Summe zweier Zeilen ergibt aufgrund der Linearität wieder ein Codewort von $C_1$.
- Ebenso ergibt die Summe zweier Spalten ein gültiges Codewort von $C_2$.
- Jeder Produktcodes beinhaltet auch das Nullwort $\underline{0}$ (ein Vektor mit $n$ Nullen).
- Die minimale Distanz von $C$ ist $d_{\rm min} = d_1 \cdot d_2$, wobei $d_i$ die minimale Distanz von $C_i$ angibt.
Iterative Syndromdecodierung von Produktcodes (1)
Wir betrachten nun den Fall, dass ein Produktcode mit Matrix X über einen Binärkanal übertragen wird. Die Empfangsmatrix sei Y = X + E, wobei E die Fehlermatrix bezeichnet. Alle Elemente der Matrizen X, E und Y seien binär, also 0 oder 1.
Für die Decodierung der beiden Komponentencodes bietet sich die Syndromdecodierung entsprechend dem Kapitel 1.5 an. Im zweidimensionalen Fall bedeutet dies:
- Man decodiert zunächst die n2 Zeilen der Empfangsmatrix Y, basierend auf der Prüfmatrix H1 des Komponentencodes C1. Man verwendet hierzu die Syndromdecodierung.
- Dazu bildet man jeweils das sogenannte Syndrom s = y · H1T, wobei der Vektor y der Länge n1 die aktuelle Zeile von Y angibt und „T” für „transponiert” steht.
- Entsprechend dem berechneten sμ (mit 0 ≤ μ < 2n1–k1) findet man dann in einer vorbereiteten Syndromtabelle das wahrscheinliche Fehlermuster e = eμ.
- Bei nur wenigen Fehlern innerhalb der Zeile stimmt dann y + e mit dem gesendeten Zeilenvektor x überein. Sind zu viele Fehler aufgetreten, so kommt es allerdings zu Fehlkorrekturen.
- Anschließend syndromdecodiert man die n1 Spalten der (korrigierten) Empfangsmatrix Y', diesmal basierend auf der (transponierten) Prüfmatrix H2T des Komponentencodes C2.
- Hierzu bildet man das Syndrom s = y' · H2T, wobei der Vektor y' der Länge n2 die betrachtete Spalte von Y' bezeichnet.
- Aus einer zweiten Syndromtabelle (gültig für den Code C2) findet man für das berechnete sμ (mit 0 ≤ μ < 2n2–k2) das wahrscheinliche Fehlermuster e = eμ der bearbeiteten Spalte.
- Nach Korrektur aller Spalten liegt die Marix Y vor. Nun kann man wieder eine Zeilen– und anschließend eine Spaltendecodierung vornehmen ⇒ zweite Iteration, und so weiter, und so fort.
Auf der nächsten Seite wird dieser Decodieralgorithmus an einem Beispiel verdeutlicht. Dazu betrachten wir wieder den (42, 12) Produktcode, basierend auf
- dem Hammingcode (7, 4, 3) ⇒ Code C1,
- dem verkürzten Hammingcode (6, 3, 3) ⇒ Code C2.
Die Prüfmatrizen dieser beiden systematischen Komponentencodes lauten in transponierter Form:
\[{ \boldsymbol{\rm H}}_1^{\rm T} =
\begin{pmatrix}
1 &0 &1 \\
1 &1 &0 \\
0 &1 &1 \\
1 &1 &1 \\
1 &0 &0 \\
0 &1 &0 \\
0 &0 &1
\end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm}
{ \boldsymbol{\rm H}}_2^{\rm T} =
\begin{pmatrix}
1 &1 &0 \\
1 &0 &1 \\
0 &1 &1 \\
1 &0 &0 \\
0 &1 &0 \\
0 &0 &1
\end{pmatrix}\hspace{0.05cm}.\]
Iterative Syndromdecodierung von Produktcodes (2)
Die linke Grafik zeigt die Empfangsmatrix Y, Aus Darstellungsgründen wurde die Codermatrix X zu einer 6 × 7–Nullmatrix gewählt, so dass die neun Einsen in Y gleichzeitig Übertragungsfehler darstellen.
Hinweis: Für die folgenden Berechnungen ist der Link zu den transponierten Prüfmatrizen nützlich.
Die zeilenweise Syndromdecodierung geschieht über das Syndrom s = y · H1T. Im Einzelnen:
- \[\underline{s} = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right ) = \underline{s}_3\]
- \[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_3 = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.\]
- Zeile 2 ⇒ Fehlkorrektur bezüglich Bit 5:
- \[\underline{s} = \left ( 1, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right ) = \underline{s}_4\]
- \[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_4 = \left ( 1, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}1 \right ) \hspace{0.05cm}.\]
- Zeile 5 ⇒ Fehlkorrektur bezüglich Bit 3:
- \[\underline{s} = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right ) = \underline{s}_3\]
- \[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_3 = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.\]
Die spaltenweisen Syndromdecodierung entfernt alle Einzelfehler in den Spalten 1, 2, 3, 4, 6 und 7.

- Spalte 5 ⇒ Fehlkorrektur bezüglich Bit 4:
- \[\underline{s} = \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right ) = \underline{s}_4\]
- \[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_4 = \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.\]
Die verbliebenen drei Fehler werden durch zeilenweise Decodierung der zweiten Iterationsschleife korrigiert.
Ob alle Fehler eines Blockes korrigierbar sind, hängt vom Fehlermuster ab. Hier verweisen wir auf Aufgabe A4.7.
Leistungsfähigkeit der Produktcodes
Die 1954 eingeführten Produktcodes waren die ersten Codes, die auf rekursiven Konstruktionsregeln basierten und somit grundsätzlich für die iterative Decodierung geeignet waren. Der Erfinder Peter Elias hat sich diesbezüglich zwar nicht geäußert, aber in den letzten zwanzig Jahren hat dieser Aspekt und die gleichzeitige Verfügbarkeit schneller Prozessoren dazu beigetragen, dass inzwischen auch Produktcodes in realen Kommunikationssystemen eingesetzt werden, z. B. beim Fehlerschutz von Speichermedien und bei Glasfasersystemen mit sehr hoher Datenrate.
Meist verwendet man sehr lange Produktcodes (großes n = n1 · n2) mit folgender Konsequenz:
- Aus Aufwandsgründen ist hier die Maximum–Likelihood–Decodierung auf Blockebene für die Komponentencodes C1 und C2 nicht anwendbar, auch nicht die Syndromdecodierung, die ja eine Realisierungsform der ML–Decodierung darstellt.
- Anwendbar ist dagegen auch bei großem n die iterative symbolweise MAP–Decodierung, wie in Kapitel 4.1 beschrieben. Der Austausch von extrinsischer und Apriori–Information geschieht hier zwischen den beiden Komponentencodes. Genaueres hierüber findet man in [Liv15][1].
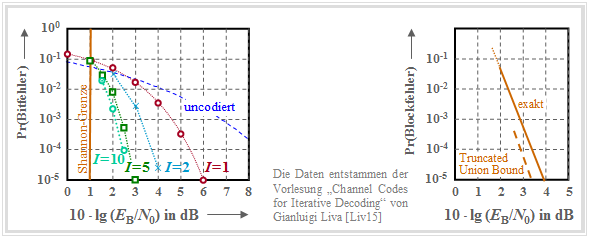
Die Grafik zeigt für einen (1024, 676)–Produktcode, basierend auf dem Extended Hammingcode eHC (32, 26) als Komponentencodes, die AWGN–Bitfehlerwahrscheinlichkeit (links) in Abhängigkeit der Iterationen (I) sowie rechts die Fehlerwahrscheinlichkeit der Blöcke (bzw. Codeworte). Die Coderate beträgt R = R1 · R2 = 0.66, womit sich die Shannon–Grenze zu 10 · lg (EB/N0) ≈ 1 dB ergibt.
Links erkennt man den Einfluss der Iterationen. Beim Übergang von I = 1 auf I gewinnt man ca. 2 dB (bei der Bitfehlerrate 10–5) und mit I = 10 ein weiteres dB. Weitere Iterationen lohnen sich nicht.
Auch alle in Kapitel 1.6 genannten Schranken können hier angewendet werden, so auch die in der rechten Grafik gestrichelt eingezeichneten Truncated Union Bound:
\[{\rm Pr(Truncated{0.15cm}Union\hspace{0.15cm} Bound)}= W_{d_{\rm min}} \cdot {\rm Q} \left ( \sqrt{d_{\rm min} \cdot {2R \cdot E_{\rm B}}/{N_0}} \right ) \hspace{0.05cm}.\]
Die minimale Distanz beträgt dmin = d1 · d2 = 4 · 4 = 16. Mit der Gewichtsfunktion des eHC (32, 26),
\[W_{\rm eHC(32,\hspace{0.08cm}26)}(X) = 1 + 1240 \cdot X^{4} + 27776 \cdot X^{6}+ 330460 \cdot X^{8} + ...\hspace{0.05cm} + X^{32},\]
erhält man für den Produktcode Wd, min = 12402 = 15376000. Damit ist die obere Gleichung bestimmt.
Aufgaben
Zusatzaufgaben:Z4.6: Grundlagen der Produktcodes
Zusatzaufgaben:Z4.7: Syndromdecodierung – Prinzip
Quellenverzeichnis
- ↑ Liva, G.: Channels Codes for Iterative Decoding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2015.