Difference between revisions of "Aufgaben:Exercise 3.6: State Transition Diagram"
From LNTwww
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm }} [[File:|right|]] ===Fragebogen=== <quiz display=simple…“) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm | + | {{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm}} |
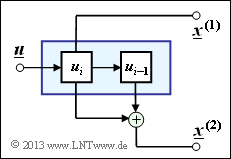
| + | [[File:P_ID2648__KC_A_3_6.png|right|frame|Einfacher Rate–1/2–Faltungscodierer]] | ||
| + | Eine Beschreibungsmöglichkeit für Faltungscodierer bietet das so genannte <i>Zustandsübergangsdiagramm</i>- Beinhaltet der Coder $m$ Speicherregister ⇒ Einflusslänge $\nu = m + 1$, so gibt es nach der aktuellen Speicherbelegung verschiedene Zustände $S_{\mu}$ mit $0 ≤ \mu ≤ 2^m \, –1$, wobei für den Index gilt: | ||
| + | :$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | Diese Art der Coderbeschreibung soll auf den oben skizzierten Faltungscodierer der Rate $R = 1/2$ angewendet werden. | ||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm| Codebeschreibung mit Zustands– und Trellisdiagramm]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $xyz \ = \ ${ 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
| − | '''2 | + | '''(2)''' |
| − | '''3 | + | '''(3)''' |
| − | '''4 | + | '''(4)''' |
| − | '''5 | + | '''(5)''' |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 12:23, 30 November 2017
Eine Beschreibungsmöglichkeit für Faltungscodierer bietet das so genannte Zustandsübergangsdiagramm- Beinhaltet der Coder $m$ Speicherregister ⇒ Einflusslänge $\nu = m + 1$, so gibt es nach der aktuellen Speicherbelegung verschiedene Zustände $S_{\mu}$ mit $0 ≤ \mu ≤ 2^m \, –1$, wobei für den Index gilt:
- $$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$
Diese Art der Coderbeschreibung soll auf den oben skizzierten Faltungscodierer der Rate $R = 1/2$ angewendet werden.
Hinweis:
- Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)