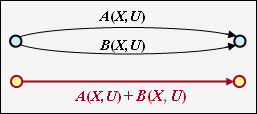Difference between revisions of "Channel Coding/Distance Characteristics and Error Probability Bounds"
| Line 10: | Line 10: | ||
Eine äußerst wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit eines linearen Blockcodes ist die <i>minimale Distanz</i> zwischen zwei Codeworten: | Eine äußerst wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit eines linearen Blockcodes ist die <i>minimale Distanz</i> zwischen zwei Codeworten: | ||
| − | :<math>d_{\rm min}(\mathcal{C}) = | + | ::<math>d_{\rm min}(\mathcal{C}) = |
\min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') | ||
= | = | ||
| Line 18: | Line 18: | ||
Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort $(\underline{0})$ beinhaltet. Zweckmäßigerweise setzt man deshalb $\underline{x}' = \underline{0}$, so dass die [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Distanz]] $d_{\rm H}(\underline{x}, \ \underline{0})$ das gleiche Ergebnis liefert wie das Hamming–Gewicht $w_{\rm H}(\underline{x})$.<br> | Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort $(\underline{0})$ beinhaltet. Zweckmäßigerweise setzt man deshalb $\underline{x}' = \underline{0}$, so dass die [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Distanz]] $d_{\rm H}(\underline{x}, \ \underline{0})$ das gleiche Ergebnis liefert wie das Hamming–Gewicht $w_{\rm H}(\underline{x})$.<br> | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 1:}$ Die folgende Tabelle zeigt die 16 Codeworte des [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Einige_Eigenschaften_des_.287.2C_4.2C_3.29.E2.80.93Hamming.E2.80.93Codes| (7, 4, 3)–Hamming–Codes]].<br> | ||
| − | [[File:P ID2684 KC T 3 5 S1 neu.png|center|frame| Codewort des $(7, 4, 3)$–Hamming–Codes|class=fit]] | + | [[File:P ID2684 KC T 3 5 S1 neu.png|center|frame| Codewort des $(7, 4, 3)$–Hamming–Codes|class=fit]] |
| − | Alle Codeworte außer dem Nullwort $(\underline{0})$ beinhalten mindestens drei Einsen ⇒ $d_{\rm min} = 3$. Es gibt sieben Codeworte mit drei Einsen, sieben mit vier Einsen und je eines ohne Einsen bzw. mit sieben Einsen. | + | Alle Codeworte außer dem Nullwort $(\underline{0})$ beinhalten mindestens drei Einsen ⇒ $d_{\rm min} = 3$. Es gibt sieben Codeworte mit drei Einsen, sieben mit vier Einsen und je eines ohne Einsen bzw. mit sieben Einsen.}}<br> |
Die <b>freie Distanz</b> $d_{\rm F}$ eines Faltungscodes (<i>Convolution Code</i> ⇒ ${\rm CC}$) unterscheidet sich formelmäßig nicht von der minimalen Distanz eines linearen Blockcodes: | Die <b>freie Distanz</b> $d_{\rm F}$ eines Faltungscodes (<i>Convolution Code</i> ⇒ ${\rm CC}$) unterscheidet sich formelmäßig nicht von der minimalen Distanz eines linearen Blockcodes: | ||
Revision as of 16:08, 2 December 2017
Contents
- 1 Freie Distanz vs. Minimale Distanz
- 2 Pfadgewichtsfunktion (1)
- 3 Pfadgewichtsfunktion (2)
- 4 Erweiterte Pfadgewichtsfunktion
- 5 Pfadgewichtsfunktion aus Zustandsübergangsdiagramm (1)
- 6 Pfadgewichtsfunktion aus Zustandsübergangsdiagramm (2)
- 7 Pfadgewichtsfunktion aus Zustandsübergangsdiagramm (3)
- 8 Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke (1)
- 9 Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke (2)
- 10 Bitfehlerwahrscheinlichkeit und Viterbi–Schranke (1)
- 11 Bitfehlerwahrscheinlichkeit und Viterbi–Schranke (2)
- 12 Aufgaben
Freie Distanz vs. Minimale Distanz
Eine äußerst wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit eines linearen Blockcodes ist die minimale Distanz zwischen zwei Codeworten:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]
Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort $(\underline{0})$ beinhaltet. Zweckmäßigerweise setzt man deshalb $\underline{x}' = \underline{0}$, so dass die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{0})$ das gleiche Ergebnis liefert wie das Hamming–Gewicht $w_{\rm H}(\underline{x})$.
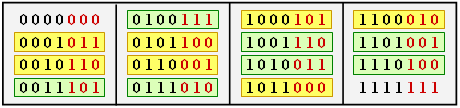
$\text{Beispiel 1:}$ Die folgende Tabelle zeigt die 16 Codeworte des (7, 4, 3)–Hamming–Codes.
Alle Codeworte außer dem Nullwort $(\underline{0})$ beinhalten mindestens drei Einsen ⇒ $d_{\rm min} = 3$. Es gibt sieben Codeworte mit drei Einsen, sieben mit vier Einsen und je eines ohne Einsen bzw. mit sieben Einsen.
Die freie Distanz $d_{\rm F}$ eines Faltungscodes (Convolution Code ⇒ ${\rm CC}$) unterscheidet sich formelmäßig nicht von der minimalen Distanz eines linearen Blockcodes:
\[d_{\rm F}(\mathcal{CC}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]
In der Literatur wird anstelle von $d_{\rm F}$ teilweise auch $d_{∞}$ verwendet.
- Wesentlicher Unterschied zur minimalen Distanz ist, dass bei Faltungscodes nicht Informations– und Codeworte zu betrachten sind, sondern Sequenzen mit der Eigenschaft Kanalcodierung/Grundlagen der Faltungscodierung.
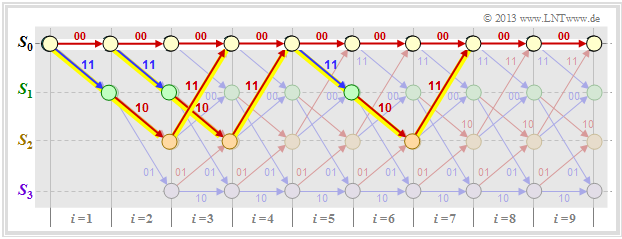
- Jede Codesequenz $\underline{x}$ beschreibt einen Pfad durch das Trellis. Die freie Distanz ist dabei das kleinstmögliche Hamming–Gewicht eines solchen Pfades (mit Ausnahme des Nullpfades).
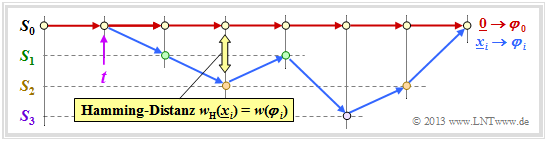
Die Grafik zeigt drei der unendlich vielen Pfade mit dem minimalen Hamming–Gewicht $w_{\rm H}(\underline{x}) = d_{\rm F} = 5$.
Pfadgewichtsfunktion (1)
Für jeden linearen Blockcode lässt sich wegen der endlichen Anzahl an Codeworten $\underline{x}$ in einfacher Weise eine Gewichtsfunktion angeben. Für das Beispiel auf der letzten Seite lautet diese:
\[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]
Bei einem (nicht terminierten) Faltungscode kann keine solche Gewichtsfunktion angegegeben werden, da es unendlich viele, unendlich lange Codesequenzen $\underline{x}$ gibt, und damit auch unendlich viele Trellispfade. Um dieses Problem in den Griff zu bekommen, gehen wir nun von folgenden Voraussetzungen aus:
- Als Bezugsgröße für das Trellisdiagramm wählen wir stets den Pfad der Codesequenz $\underline{x} = \underline{0}$ und nennen diesen den Nullpfad $\varphi_0$.
- Desweiteren betrachten wir nur noch solche Pfade $\varphi_j ∈ {\it \Phi}$, die alle zu einer vorgegebenen Zeit $t$ vom Nullpfad abweichen und irgendwann wieder zu diesem zurückkehren.
Obwohl nur ein Bruchteil aller Trellispfade zu dieser Menge ${\it \Phi}$ gehören, beinhaltet ${\it \Phi} = \{\varphi_1, \ \varphi_2, \ \varphi_3, \ ...\}$ noch immer eine unbegrenzte Menge an Pfaden. $\varphi_0$ gehört nicht zu dieser Menge.
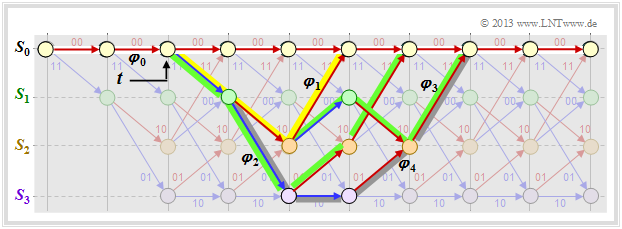
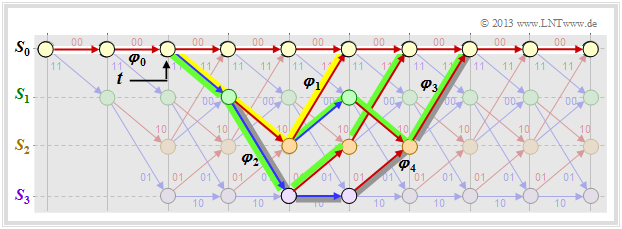
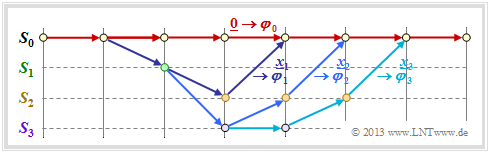
Im obigen Trellis sind einige Pfade $\varphi_j ∈ {\it \Phi}$ eingezeichnet:
- Der gelbe Pfad $\varphi_1$ gehört zur Sequenz $\underline{x}_1 = (11, 10, 11)$ mit dem Hamming–Gewicht $w_{\rm H}(\underline{x}_1) = 5$. Damit ist auch das Pfadgewicht $w(\varphi_1) = 5$. Aufgrund der Festlegung des Abzweigzeitpunktes $t$ hat nur noch dieser einzige Pfad $\varphi_1$ die freie Distanz $d_{\rm F} = 5$ zum Nullpfad ⇒ $A_5 = 1$.
- Für die beiden grünen Pfade mit den korrespondierenden Sequenzen $\underline{x}_2 = (11, 01, 01, 11)$ bzw. $\underline{x}_3 = (11, 10, 00, 10, 11)$ gilt $w(\varphi_2) = w(\varphi_3) = 6$. Kein anderer Pfad weist das Pfadgewicht $6$ auf. Wir berücksichtigen diese Tatsache durch den Koeffizienten $A_6 = 2$.
- Eingezeichnet ist auch der graue Pfad $\varphi_4$, assoziiert mit der Sequenz $\underline{x}_4 = (11, 01, 10, 01, 11)$ ⇒ $w(\varphi_4) = 7$. Auch die Sequenzen $\underline{x}_5 = (11, 01, 01, 00, 10, 11), \ \underline{x}_6 = (11, 10, 00, 01, 01, 11)$ und $\underline{x}_7 = (11, 10, 00, 10, 00, 10, 11)$ weisen jeweils das gleiche Pfadgewicht $7$ auf ⇒ $A_7 = 4$.
Damit lautet die Pfadgewichtsfunktion (englisch: Path Weight Enumerator Function, PWEF):
\[T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + ... \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ ... \hspace{0.1cm} \hspace{0.05cm}.\]
Die Definition dieser Funktion $T(X)$ wird auf der nächsten Seite nachgeliefert.
Pfadgewichtsfunktion (2)
\[T(X) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w = d_{\rm F}}^{\infty}\hspace{0.1cm} A_w \cdot X^w \hspace{0.05cm}.\]
- ${\it \Phi}$ bezeichnet die Menge aller Pfade an, die den Nullpfad $\varphi_0$ genau zum festgelegten Zeitpunkt $t$ verlassen und (irgendwann) später zu diesem zurückkehren.
- Gemäß der zweiten Gleichung sind die Summanden nach ihren Pfadgewichten $w$ geordnet, wobei $A_w$ die Anzahl der Pfade mit Pfadgewicht $w$ bezeichnet. Die Summe beginnt mit $w = d_{\rm F}$.
- Das Pfadgewicht $w(\varphi_j)$ ist gleich dem Hamming–Gewicht (also der Anzahl der Einsen) der zum Pfad $\varphi_j$ assoziierten Codesequenz $\underline{x}_j$:
- \[w({\varphi_j) = w_{\rm H}(\underline {x}}_j) \hspace{0.05cm}.\]
Hinweis: Die für die linearen Blockcodes definierte Gewichtsfunktion $W(X)$ und die hier
definierte Pfadgewichtsfunktion $T(X)$ weisen viele Gemeinsamkeiten auf, sie sind jedoch nicht identisch.
Betrachten wir nochmals die Gewichtsfunktion
\[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\]
des $(7, 4, 3)$–Hamming–Codes und die Pfadgewichtsfunktion
\[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ ... \]
unseres Standard–Faltungscodierers, so fällt die „$1$” in der ersten Gleichung auf. Das heißt: Bei den linearen Blockcodes wird das Bezugs–Codewort $\underline{x}_i = \underline{0}$ mitgezählt, wohingegen die Nullcodesequenz $\underline{x}_i = \underline{0}$ bzw. der Nullpfad $\varphi_0$ bei den Faltungscodes ausgeschlossen wird. Nach Ansicht der Autoren hätte man auch $W(X)$ ohne die „$1$” definieren können. Damit wäre unter anderem vermieden worden, dass sich die Bhattacharyya–Schranke für lineare Blockcodes und für Faltungscodes durch „$–1$” unterscheiden, wie aus den folgenden Gleichungen hervorgeht:
Bhattacharyya–Schranke für die linearen Blockcodes:
\[{\rm Pr(Blockfehler)} \le W(X = \beta) -1 \hspace{0.05cm},\]
Bhattacharyya–Schranke für die Faltungscodes:
\[{\rm Pr(Burstfehler)} \le T(X = \beta) \hspace{0.05cm},\]
Die Pfadgewichtsfunktion $T(X)$ liefert nur Informationen hinsichtlich der Gewichte der Codesequenz $\underline{x}$. Mehr Informationen erhält man, wenn zusätzlich auch die Gewichte der Informationssequenz $\underline{u}$ erfasst werden. Man benötigt dann zwei Formalparameter $X$ und $U$, wie aus der Definition auf der folgenden Seite hervorgeht.
Erweiterte Pfadgewichtsfunktion
\[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]
Es gelten alle Angaben der Definition von $T(X)$ auf der letzten Seite. Zusätzlich ist zu beachten:
- Das Pfadeingangsgewicht $u(\varphi_j)$ ist gleich dem Hamming–Gewicht der zum Pfad $\varphi_j$ assoziierten Informationssequenz $\underline{u}_j$. Es wird als Potenz des Formalparameters $U$ ausgedrückt.
- Der Koeffizient $A_{w, \ u}$ bezeichnet die Anzahl der Pfade $\varphi_j$ mit dem Pfadausgangsgewicht $w(\varphi_j)$ und dem Pfadeingangsgewicht $u(\varphi_j)$. Als Laufvariable für den zweiten Anteil wird $u$ verwendet.
- Setzt man in der erweiterten Pfadgewichtsfunktion den Formalparameter $U = 1$, so ergibt sich die ursprüngliche Gewichtsfunktion $T(X)$ gemäß der Definition auf der letzten Seite.
Bei vielen (und allen relevanten) Faltungscodes lässt sich obere Gleichung noch vereinfachen:
\[T_{\rm enh}(X, U) =\hspace{0.1cm} \sum_{w = d_{\rm F}}^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]
Die erweiterte Pfadgewichtsfunktion unseres Standardcodieres lautet somit:
\[T_{\rm enh}(X, U) = U \cdot X^5 + 2 \cdot U^2 \cdot X^6 + 4 \cdot U^3 \cdot X^7+ ... \hspace{0.1cm} \hspace{0.05cm}.\]
Vergleicht man dieses Ergebnis mit dem unten dargestellten Trellis, so erkennt man:
- Der gelb hinterlegte Pfad – gekennzeichnet durch $X^5$ – setzt sich aus einem blauen Pfeil $(u_i = 1)$ und zwei roten Pfeilen $(u_i = 0)$ zusammen. Somit wird aus $X^5$ der erweiterte Term $UX^5$.
- Die Sequenzen der beiden grünen Pfade sind $\underline{u}_2 = (1, 1, 0, 0)$ ⇒ $\underline{x}_2 = (11, 01, 01, 11)$ sowie $\underline{u}_3 = (1, 0, 1, 0, 0)$ ⇒ $\underline{x}_3 = (11, 10, 00, 10, 11)$. Daraus ergibt sich der zweite Term $2 \cdot U^2X^6$.
- Der graue Pfad (und die drei nicht gezeichneten Pfade) ergeben zusammen den Beitrag $4 \cdot U^3X^7$. Jeder dieser Pfade beinhaltet drei blaue Pfeile ⇒ drei Einsen in jeder Informationssequenz.
Pfadgewichtsfunktion aus Zustandsübergangsdiagramm (1)
Es gibt eine elegante Methode, um die Pfadgewichtsfunktion $T(X)$ und deren Erweiterung direkt aus dem Zustandsübergangsdiagramm zu bestimmen. Dies soll hier und auf den folgenden Seiten am Beispiel unseres Standardcodes demonstriert werden.
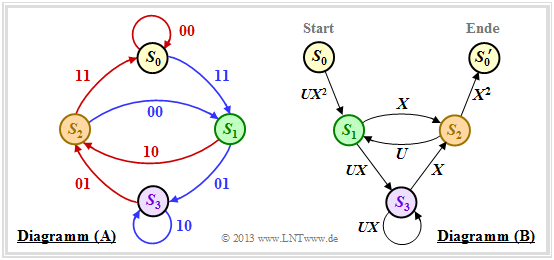
Zunächst muss dazu das Zustandsübergangsdiagramm umgezeichnet werden. Die Grafik zeigt dieses links in der bisherigen Form als Diagramm (A), während rechts das neue Diagramm (B) angegeben ist.
Man erkennt:
- Der Zustand $S_0$ wird aufgespalten in den Startzustand $S_0$ und den Endzustand $S_0'$. Damit lassen sich alle Pfade des Trellisdiagramms, die im Zustand $S_0$ beginnen und irgendwann zu diesem zurückkehren, auch im rechten Graphen (B) nachvollziehen. Ausgeschlossen sind dagegen direkte Übergänge von $S_0$ nach $S_0'$ und damit auch der Nullpfad (Dauer–$S_0$).
- Im Diagramm (A) sind die Übergänge anhand der Farben Rot (für $u_i = 0$) und Blau (für $u_i = 1$) unterscheidbar, und die Codeworte $\underline{x}_i ∈ \{00, 01, 10, 11\}$ sind an den Übergängen vermerkt. Im neuen Diagramm (B) werden $(00)$ durch $X^0 = 1$ und $(11)$ durch $X^2$ ausgedrückt. Die Codeworte $(01)$ und $(10)$ sind nun nicht mehr unterscheidbar, sondern werden einheitlich mit $X$ bezeichnet.
- Anders formuliert: Das Codewort $\underline{x}_i$ wird nun als $X^w$ dargestellt, wobei $X$ eine dem Ausgang (der Codesequenz) zugeordnete Dummy–Variable ist und $w = w_{\rm H}(\underline{x}_i)$ das Hamming–Gewicht des Codewortes $\underline{x}_i$ angibt. Bei einem Rate–$1/2$–Code ist der Exponent $w$ entweder $0, 1$ oder $2$.
- Ebenfalls verzichtet wird im Diagramm (B) auf die Farbcodierung. Das Informationsbit $u_i = 1$ wird nun durch $U^1 = U$ und das Informationsbit $u_i = 0$ durch $U^0 = 1$ gekennzeichnet. Die Dummy–Variable $U$ ist also der Eingangssequenz $\underline{u}$ zugeordnet.
Die Beschreibung wird auf den nächsten Seiten fortgesetzt.
Pfadgewichtsfunktion aus Zustandsübergangsdiagramm (2)
Ziel unserer Berechnungen wird es sein, den (beliebig komplizierten) Weg von $S_0$ nach $S_0'$ durch die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \ U)$ zu charakterisieren. Dazu benötigen wir Regeln, um den Graphen schrittweise vereinfachen zu können.
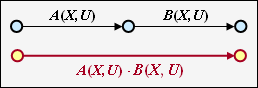
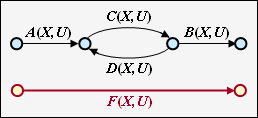
Serielle Übergänge
Zwei serielle Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – können durch eine einzige Verbindung mit dem Produkt dieser Bewertungen ersetzt werden.
Parallele Übergänge
Zwei parallele Verbindungen werden durch die Summe ihrer Bewertungsfunktionen zusammengefasst.
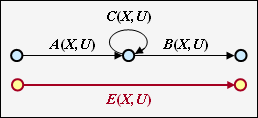
Ring Die nebenstehende Konstellation kann durch eine einzige Verbindung ersetzt werden, wobei für die Ersetzung gilt:
\[E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)}
\hspace{0.05cm}.\]
Rückkopplung
Durch die Rückkopplung können sich hier zwei Zustände beliebig oft abwechseln. Für diese Konstellation gilt:
\[F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} \hspace{0.05cm}.\]
Die hier angegebenen Gleichungen für Ring und Rückkopplung sind in Aufgabe Z3.12 zu beweisen.
Pfadgewichtsfunktion aus Zustandsübergangsdiagramm (3)
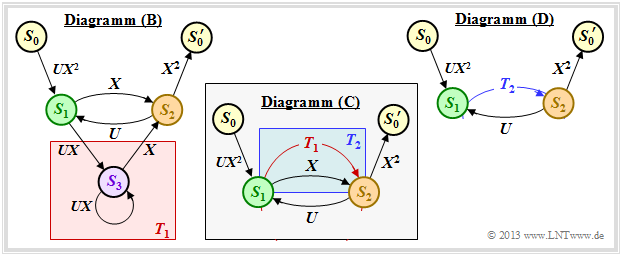
Die auf der letzten Seite genannten Regeln sollen nun auf unser Standardbeispiel angewendet werden. In der unteren Grafik sehen Sie links das modifizierte Zustandsübergangsdiagramm (B).
- Zunächst ersetzen wir den rot hinterlegten Umweg von $S_1$ nach $S_2$ über $S_3$ im Diagramm (B) durch die im Diagramm (C) eingezeichnete rote Verbindung. Es handelt sich nach der Klassifizierung auf der letzten Seite um einen „Ring” mit den Beschriftungen $A = C = U \cdot X$ und $B = X$, und wir erhalten die erste Reduktionsfunktion:
- \[T_1(X, U) = \frac{U \cdot X^2}{1- U \cdot X} \hspace{0.05cm}.\]
- Nun fassen wir die parallelen Verbindungen entsprechend der blauen Hinterlegung im Diagramm (C) zusammen und ersetzen diese durch die blaue Verbindung im Diagramm (D). Die zweite Reduktionsfunktion lautet somit:
- \[T_2(X, U) = T_1(X, U) + X = \frac{U X^2 + X \cdot (1-UX)}{1- U X} = \frac{X}{1- U X} \hspace{0.05cm}.\]
- Der gesamte Graph (D) kann somit durch eine einzige Verbindung von $S_0$ nach $S_0'$ ersetzt werden. Nach der Rückkopplungsregel erhält man für die erweiterte Pfadgewichtsfunktion:
- \[T_{\rm enh}(X, U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X}}{1- U \cdot \frac{X}{1- U X}} = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} \hspace{0.05cm}.\]
Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ ... \ $ lässt sich hierfür auch schreiben:
\[T_{\rm enh}(X, U) = U X^5 \cdot \left [ 1 + 2 \hspace{0.05cm}UX + (2 \hspace{0.05cm}UX)^2 + (2 \hspace{0.05cm}UX)^3 + ... \hspace{0.05cm} \right ] \hspace{0.05cm}.\]
Setzt man die formale Input–Variable $U = 1$, so erhält man die „einfache” Pfadgewichtsfunktion, die allein Aussagen über die Gewichtsverteilung der Ausgangssequenz $\underline{x}$ erlaubt:
\[T(X) = X^5 \cdot \left [ 1 + 2 X + 4 X^2 + 8 X^3 + ... \hspace{0.05cm} \right ] \hspace{0.05cm}.\]
Das gleiche Ergebnis haben wir bereits aus dem Trellisdiagramm auf Seite 2a abgelesen. Dort gab es einen grauen Pfad mit Gewicht $5$, zwei gelbe Pfade mit Gewicht $6$ und vier grüne Pfade mit Gewicht $7$.
Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke (1)
Das folgende einfache Modell gilt sowohl für lineare Blockcodes als auch für Faltungscodes.
Bei den Blockcodes bezeichnen $\underline{u} = (u_1, \ ... , \ u_i, \ ..., \ u_k)$ und $\underline{\upsilon} = (\upsilon_1, \ ..., \ \upsilon_i, \ ... \ , \ \upsilon_k)$ die Informationsblöcke am Eingang und Ausgang des Systems. Damit können folgende Beschreibungsgrößen definiert werden:
- die Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{\upsilon} ≠ \underline{u}),$
- die Bitfehlerwahrscheinlichkeit ${\rm Pr}(\upsilon_i ≠ u_i).$
Bei realen Übertragungssystemen ist aufgrund des thermischen Rauschens die Bitfehlerwahrscheinlichkeit stets größer als $0$. Weiter gilt:
\[{\rm Pr(Blockfehler)} > {\rm Pr(Bitfehler)} \hspace{0.05cm}.\]
Hierfür ein einfacher Erklärungsversuch: Entscheidet der Decoder in jedem Block der Länge $k \ \rm Bit$ genau ein $\rm Bit$ falsch, so beträgt die Bitfehlerwahrscheinlichkeit $= 1/k$ und die Blockfehlerwahrscheinlichkeit ist $1$.
Bei Faltungscodes ist dagegen die Blockfehlerwahrscheinlichkeit nicht angebbar, da hier $\underline{u} = (u_1, \ u_2, \ ...)$ und $\underline{\upsilon} = (\upsilon_1, \ \upsilon_2, \ ...)$ Sequenzen darstellen. Selbst der kleinstmögliche Codeparameter $k = 1$ führt hier zur Sequenzlänge $k' → ∞$, und die Blockfehlerwahrscheinlichkeit ergäbe sich stets zu $1$, selbst wenn die Bitfehlerwahrscheinlichkeit extrem klein (aber $≠ 0$) ist.
Deshalb definieren wir bei Faltungscodes stattdessen die Burstfehlerwahrscheinlichkeit:
\[{\rm Pr(Burstfehler)} = {\rm Pr}\big \{{\rm Decoder\hspace{0.15cm} verl\ddot{a}sst\hspace{0.15cm} zur\hspace{0.15cm} Zeit}\hspace{0.15cm}t \hspace{0.15cm}{\rm den \hspace{0.15cm}korrekten \hspace{0.15cm}Pfad}\big \} \hspace{0.05cm}.\]
Um für die folgende Herleitung die Schreibweise zu vereinfachen, gehen wir stets von der Nullsequenz $(\underline{0})$ aus, die im gezeichneten Trellis als Nullpfad $\varphi_0$ rot dargestellt ist. Alle anderen eingezeichneten Pfade $\varphi_1, \ \varphi_2, \ \varphi_3, \ ... \ $ (und noch viele mehr) verlassen $\varphi_0$ zur Zeit $t$. Sie alle gehören zur Pfadmenge ${\it \Phi}$ ⇒ „Viterbi–Decoder verlässt den korrekten Pfad zur Zeit $t$”, deren Wahrscheinlichkeit auf der nächsten Seite berechnet werden soll.
Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke (2)
Wir gehen wie in Kapitel 1.6 von der paarweisen Fehlerwahrscheinlichkeit ${\rm Pr}[\varphi_0 → \varphi_i]$ aus, dass vom Decoder anstelle des Pfades $\varphi_0$ der Pfad $\varphi_i$ ausgewählt werden könnte. Alle betrachteten Pfade $\varphi_i$ haben gemein, dass sie den Nullpfad $\varphi_0$ zum Zeitpunkt $t$ verlassen; sie gehören alle zur Pfadmenge ${\it \Phi}$.
Die gesuchte Burstfehlerwahrscheinlichkeit ist gleich der folgenden Vereinigungsmenge:
\[{\rm Pr(Burstfehler)}= {\rm Pr}\left ([\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}]\hspace{0.05cm}\cup\hspace{0.05cm} ...\hspace{0.05cm} \right )= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}] \right )\hspace{0.05cm}.\]
Eine obere Schranke hierfür bietet die so genannte Union–Bound entsprechend Kapitel 1.6:
\[{\rm Pr(Burstfehler)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] = {\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{0.05cm}.\]
Die paarweise Fehlerwahrscheinlichkeit kann mit der Bhattacharyya–Schranke abgeschätzt werden:
\[{\rm Pr}\left [\underline {0} \mapsto \underline {x}_{\hspace{0.02cm}i}\right ] \le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] \le \hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.\]
$w_{\rm H}(\underline{x}_i)$ bezeichnet das Hamming–Gewicht der möglichen Codesequenz $\underline{x}_i, \ w(\varphi_i)$ das Pfadgewicht des entsprechenden Pfades $\varphi_i ∈ {\it \Phi}$ und $\beta$ den so genannten Bhattacharyya–Kanalparameter.
Durch Summation über alle Pfade und einen Vergleich mit der (einfachen) Pfadgewichtsfunktion $T(X)$ erhalten wir das Ergebnis:
\[{\rm Pr(Burstfehler)} \le T(X = \beta),\hspace{0.5cm}{\rm mit}\hspace{0.5cm}
T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm}
\hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.\]
\[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + ... \hspace{0.1cm} = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ ... \hspace{0.1cm}) \hspace{0.05cm}.\]
Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ ... \ $ kann hierfür auch geschrieben werden:
\[T(X) = \frac{X^5}{1-2 \cdot X} \hspace{0.05cm}.\]
Das BSC–Modell liefert mit der Verfälschungswahrscheinlichkeit $\epsilon$ folgende Bhattacharyya–Schranke:
\[{\rm Pr(Burstfehler)} \le T(X = \beta) = T( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}) = \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.\]
In Aufgabe A3.14 soll diese Gleichung numerisch ausgewertet werden.
Bitfehlerwahrscheinlichkeit und Viterbi–Schranke (1)
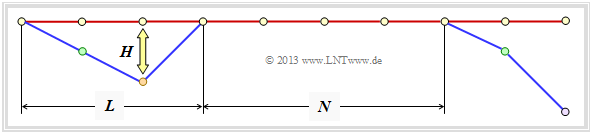
Abschließend wird eine obere Schranke für die Bitfehlerwahrscheinlichkeit angegeben. Entsprechend der Grafik gehen wir wie [Liv10] von folgenden Gegebenheiten aus:
- Gesendet wurde die Nullsequenz $\underline{x} = \underline{0}$ ⇒ Pfad $\varphi_0$.
- Die Dauer einer Pfadabweichung (englisch: Error Burst Duration) wird mit $L$ bezeichnet.
- Den Abstand zweier Bursts (englisch: Inter–Burst Time) nennen wir $N$.
- Das Hamming–Gewicht des Fehlerbündels sei $H$.
Für einen Rate–$1/n$–Faltungscode ⇒ $k = 1$, also einem Informationsbit pro Takt, lässt sich aus den Erwartungswerten $E[L], \ E[N]$ und $E[H]$ der oben definierten Zufallsgrößen eine obere Schranke für die Bitfehlerwahrscheinlichkeit angeben:
\[{\rm Pr(Bitfehler)} = \frac{{\rm E}[H]}{{\rm E}[L] + {\rm E}[N]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}[H]}{{\rm E}[N]} \hspace{0.05cm}.\]
Hierbei ist vorausgesetzt, dass die (mittlere) Dauer eines Fehlerbündels in der Praxis sehr viel kleiner ist als der zu erwartende Abstand zweier Bündel. Weiter kann gezeigt werden, dass die mittlere Inter–Burst Time $E[N]$ gleich dem Kehrwert der Burstfehlerwahrscheinlichkeit ist, während der Erwartungswert im Zähler wie folgt abgeschätzt:
\[{\rm E}[H] \le \frac{1}{\rm Pr(Burstfehler)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]
Bei der Herleitung dieser Schranke in [Liv10] werden die paarweise Fehlerwahrscheinlichkeit ${\rm Pr}[\varphi_0 → \varphi_i]$ sowie die Bhattacharyya–Abschätzung verwendet. Damit erhält man mit
- dem Pfadeingangsgewicht $u(\varphi_i),$
- dem Pfadausgangsgewicht $w(\varphi_i),$
- dem Bhattacharyya–Parameter $\beta$.
die folgende Abschätzung für die Bitfehlerwahrscheinlichkeit:
\[{\rm Pr(Bitfehler)} \hspace{0.05cm} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.01cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]
Man nennt diese Abschätzung die Viterbi–Schranke.
Bitfehlerwahrscheinlichkeit und Viterbi–Schranke (2)
Wir erinnern uns an die erweiterte Pfadgewichtsfunktion
\[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} \hspace{0.05cm}.\]
Leitet man diese Funktion nach der Dummy–Eingangsvariablen $U$ ab, so erhält man
\[\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} \hspace{0.05cm}.\]
Schließlich setzen wir noch für die Dummy–Eingangsvariablen $U = 1$:
\[\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.\]
Man erkennt den Zusammenhang zum Ergebnis der letzten Seite.
Zusammenfassung: Die Bitfehlerwahrscheinlichkeit eines Faltungscodes kann mit der erweiterten Pfadgewichtsfunktion in geschlossener Form abgeschätzt werden:
\[{\rm Pr(Bitfehler)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1}} \hspace{0.05cm}.\]
Man spricht von der Viterbi–Schranke. Dabei leitet man die erweiterte Pfadgewichtsfunktion nach dem zweiten Parameter $U$ ab und setzt dann $X = \beta$ und $U = 1$.
In Aufgabe A3.14 werden
- die Viterbi–Schranke und
- die Bhattacharyya–Schranke
für unseren Rate–$1/2$–Standardcode sowie das BSC–Modell numerisch ausgewertet.
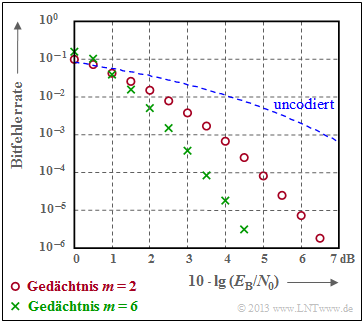
- Die roten Kreise kennzeichnen die Bitfehlerrate für den gleichen Code $(m = 2)$ beim AWGN–Kanal.
- Die grünen Kreuze markieren einen Faltungscode mit $m = 6$, den man oft Industriestandardcode nennt.
Die Grafik verdeutlicht die gute Korrekturfähigkeit der Faltungscodes. Insbesondere Codes mit großem Gedächtnis $m$ führen zu großen Gewinnen gegenüber uncodierter Übertragung (gestrichelte Kurve).
Aufgaben
Zusatzaufgaben:3.12 Ring und Rückkopplung
A3.13 Nochmals Tenh(X, U) und T(X)
A3.14 Faltungscodes: Schranken