Difference between revisions of "Aufgaben:Exercise 3.12: Path Weighting Function"
From LNTwww
| Line 2: | Line 2: | ||
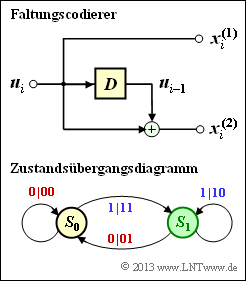
[[File:P_ID2698__KC_A_3_12.png|right|frame|Faltungscodierer mit $m = 1$ und zugehöriges Zustandsübergangsdiagramm]] | [[File:P_ID2698__KC_A_3_12.png|right|frame|Faltungscodierer mit $m = 1$ und zugehöriges Zustandsübergangsdiagramm]] | ||
| + | In [[Aufgaben:3.6_Zustands%C3%BCbergangsdiagramm|Aufgabe A3.6]] wurde das Zustandsübergangsdiagramm für den gezeichneten Faltungscoder mit den Eigenschaften | ||
| + | * Rate $R = 1/2$, | ||
| + | * Gedächtnis $m = 1$, | ||
| + | * Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1, \ ,D)$ | ||
| + | |||
| + | |||
| + | ermittelt, das ebenfalls rechts dargestellt ist. | ||
| + | |||
| + | Es soll nun aus dem Zustandsübergangsdiagramm | ||
| + | * die Pfadgewichtsfunktion $T(X)$, und | ||
| + | * die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \, U)$ | ||
| + | |||
| + | |||
| + | bestimmt werden, wobei $X$ und $U$ Dummy–Variablen sind. | ||
| + | |||
| + | Die Vorgehensweise ist im [[Theorieteil]] zu diesem Kapitel eingehend erläutert. Schließlich ist aus $T(X)$ noch die [[freie Distanz]] $d_{\rm F}$ zu bestimmen. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Themengebiet des Kapitels [[...]]. | ||
| + | * Berücksichtigen Sie bei der Lösung die Reihenentwicklung | ||
| + | :$$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \hspace{0.05cm}...\hspace{0.1cm}.$$ | ||
Revision as of 12:29, 5 December 2017
Faltungscodierer mit $m = 1$ und zugehöriges Zustandsübergangsdiagramm
In Aufgabe A3.6 wurde das Zustandsübergangsdiagramm für den gezeichneten Faltungscoder mit den Eigenschaften
- Rate $R = 1/2$,
- Gedächtnis $m = 1$,
- Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1, \ ,D)$
ermittelt, das ebenfalls rechts dargestellt ist.
Es soll nun aus dem Zustandsübergangsdiagramm
- die Pfadgewichtsfunktion $T(X)$, und
- die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \, U)$
bestimmt werden, wobei $X$ und $U$ Dummy–Variablen sind.
Die Vorgehensweise ist im Theorieteil zu diesem Kapitel eingehend erläutert. Schließlich ist aus $T(X)$ noch die Freie Distanz $d_{\rm F}$ zu bestimmen.
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels ....
- Berücksichtigen Sie bei der Lösung die Reihenentwicklung
- $$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \hspace{0.05cm}...\hspace{0.1cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
