Aufgaben:Exercise 3.12Z: Ring and Feedback

• Return to book

Ring und Rückkopplung im Zustandsübergangsdiagramm

Um die Pfadgewichtsfunktion $T(X)$ eines Faltungscodes aus dem Zustandsübergangsdiagramm bestimmen zu können, ist es erforderlich, das Diagramm so zu reduzieren, bis es durch eine einzige Verbindung vom Startzustand zum Endzustand dargestellt werden kann.

Im Zuge dieser Diagrammreduktion können auftreten:

• serielle und parallele Übergänge,
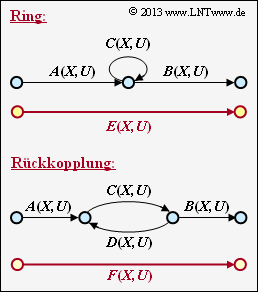
• ein Ring entsprechend der obigen Grafik,
• eine Rückkopplung entsprechend der unteren Grafik.

Für diese beiden Graphen sind die Entsprechungen $E(X, \, U)$ und $F(X, \, U)$ in Abhängigkeit der angegebenen Funktionen $A(X, \, U), \ B(X, \ U), \ C(X, \, U), \ D(X, \, U)$ zu ermitteln.

Hinweise:

• Mit dieser Aufgabe sollen einige der Angaben auf Seite 4b von Kapitel 3.5 bewiesen werden.
• Angewendet werden diese Regeln in Aufgabe A3.12 und Aufgabe A3.13.

Fragebogen

1

Welche der aufgeführten Übergänge sind beim Ring möglich?

	$S_1 → S_2 → S_3$,
	$S_1 → S_2 → S_2 → S_2 → S_3$,
	$S_1 → S_2 → S_1 → S_2 → S_3$.

2

Wie lautet die Ersetzung $E(X, \, U)$ eines Ringes?

	$E(X, \, U) = [A(X, \, U) + B(X, \, U)] \ / \ [1 \, –C(X, \, U)]$,
	$E(X, \, U) = A(X, \, U) \cdot B(X, \, U) \ / \ [1 \, –C(X, \, U)]$,
	$E(X, \, U) = A(X, \, U) \cdot C(X, \, U) \ / \ [1 \, –B(X, \, U)]$.

3

Welche der aufgeführten Übergänge sind bei Rückkopplung möglich?

	$S_1 → S_2 → S_3 → S_4$,
	$S_1 → S_2 → S_3 → S_2 → S_4$,
	$S_1 → S_2 → S_3 → S_2 → S_3 → S_4$,
	$S_1 → S_2 → S_3 → S_2 → S_3 → S_2 → S_3 → S_4$.

4

Wie lautet die Ersetzung $F(X, \, U)$ einer Rückkopplung?

	$F(X, \, U) = A(X, \, U) \cdot B(X, \, U) \cdot C(X, \, U) \ / \ [1 \, –C(X, \, U) \cdot D(X, \, U)]$
	$F(X, \, U) = A(X, \, U) \cdot B(X, \, U) \ / \ [1 \, –C(X, \, U) + D(X, \, U)]$.

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 1 und 2. Allgemein ausgedrückt: Man geht zunächst von $S_1$ nach $S_2$, verbleibt $j$–mal im Zustand $S_2 \ (j = 0, \ 1, \, 2, \ ...)$ und geht abschließend von $S_2$ nach $S_3$ weiter.

(2)  Entsprechend den Ausführungen zur Teilaufgabe (1) erhält man für die Ersetzung des Ringes

$$E \hspace{-0.15cm} & = & \hspace{-0.15cm} A \cdot B + A \cdot C \cdot B + A \cdot C^2 \cdot B + A \cdot C^3 \cdot B + ... \hspace{0.1cm}=\\ & = & \hspace{-0.15cm} A \cdot B \cdot [1 + C + C^2+ C^3 + ...\hspace{0.1cm}] \hspace{0.05cm}.$$

Der Klammerausdruck ergibt $1/(1 \, –C)$. Somit erhält man das Ergebnis gemäß Lösungsvorschlag 2.

$$E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} \hspace{0.05cm}.$$

(3)  Man geht zunächst von $S_1$ nach $S_2$ und zum Abschluss immer von $S_3$ nach $S_4$.

• Zunächst von $S_1$ nach $S_2$ \ \Rightarrow \ $A(X, \, U)$,
• dann von $S_2$ nach $S_3$ \ \Rightarrow \ $C(X, \, U)$,
• anschließend $j$–mal zurück nach $S_2$ und wieder nach $S_3 \ (j = 0, \ 1, \ 2, \ ...) \ \Rightarrow \ E(X, \, U)$,
• abschließend von $S_3$ nach $S_4 \ \Rightarrow \ B(X, \, U)$,

Richtig sind also die Lösungsvorschläge 1, 3 und 4:

(4)