Difference between revisions of "Aufgaben:Exercise 4.1: Log Likelihood Ratio"
From LNTwww
| Line 9: | Line 9: | ||
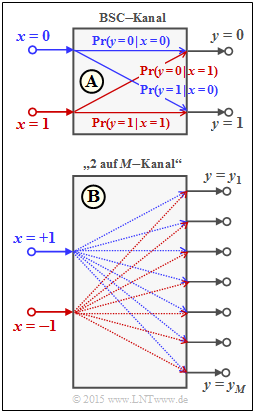
Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als [[Modell A]] bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt: | Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als [[Modell A]] bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt: | ||
| − | : | + | :$${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$ |
| − | {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} | + | :$${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$ |
Revision as of 09:13, 6 December 2017
Zur Interpretation von Log–Likelihood–Verhältnissen (kurz $L$–Werten) gehen wir wie im Theorieteil vom Binary Symmetric Channel (BSC) aus. Die englische Bezeichung ist Log Likelihood Ratio (LLR).
Für die binären Zufallsgrößen am Eingang und Ausgang gelte
- $$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}. $$
Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als Modell A bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt:
- $${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$
- $${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)