Difference between revisions of "Aufgaben:Exercise 4.2: Channel Log Likelihood Ratio at AWGN"
From LNTwww
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder}} | {{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder}} | ||
| − | [[File: | + | [[File:P_ID2980__KC_A_4_2_v2.png|right|frame|Bedingte Gaußfunktionen]] |
Wir betrachten zwei Kanäle A und B, jeweils mit | Wir betrachten zwei Kanäle A und B, jeweils mit | ||
* binärem bipolaren Eingang $x ∈ \{+1, \, –1\}$, und | * binärem bipolaren Eingang $x ∈ \{+1, \, –1\}$, und | ||
Revision as of 14:26, 6 December 2017
Wir betrachten zwei Kanäle A und B, jeweils mit
- binärem bipolaren Eingang $x ∈ \{+1, \, –1\}$, und
- wertkontinuierlichem Ausgang $y ∈ {\rm IR}$ (reelle Zahl).
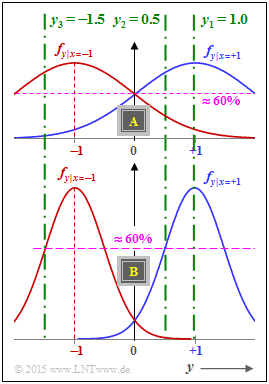
Die Grafik zeigt für beide Kanäle A und B
- als blaue Kurve die Dichtefunktionen $f_{y|x=+1}$,
- als rote Kurve die Dichtefunktionen $f_{y|x=–1}$.
Im Theorieteil wurde für diese AWGN–Konstellation der Kanal–$L$–Wert (englisch: Channel Log Likelihood Ratio, oder kurz Channel LLR) wie folgt hergeleitet:
- $$L_{\rm K}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=+1) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}.$$
Wertet man diese Gleichung analytisch aus, so erhält man mit der Proportionalitätskonstanten $K_{\rm L} = 2/\sigma^2$:
- $$L_{\rm K}(y) = K_{\rm L} \cdot y \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe gehört zum Themengebiet des Kapitels Soft–in Soft–out Decoder.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)