Difference between revisions of "Aufgaben:Exercise 4.3: Iterative Decoding at the BSC"
From LNTwww
| Line 2: | Line 2: | ||
[[File:P_ID2987__KC_A_4_3_v1.png|right|frame|BSC–Modell und mögliche Empfangswerte]] | [[File:P_ID2987__KC_A_4_3_v1.png|right|frame|BSC–Modell und mögliche Empfangswerte]] | ||
| + | Wir betrachten in dieser Aufgabe zwei Codes: | ||
| + | * den Single Parity–Code ⇒ [[SPC (3, 2, 2)]]: | ||
| + | :$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | ||
| + | (0, 1, 1), \hspace{0.1cm} | ||
| + | (1, 0, 1), \hspace{0.1cm} | ||
| + | (1, 1, 0) \hspace{0.05cm} \big ) | ||
| + | \hspace{0.05cm}, $$ | ||
| + | * den Wiederholungscode ⇒ [[RC (3, 1, 3]]: | ||
| + | :$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | ||
| + | (1, 1, 1) \hspace{0.05cm} \big ) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
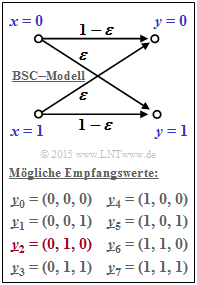
| + | Der Kanal wird auf Bitebene durch das [[BSC–Modell]] beschrieben. Entsprechend der Grafik gilt dabei: | ||
| + | :$${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei bezeichnet $\epsilon$ die Verfälschungswahrscheinlichkeit. | ||
| + | |||
| + | Bis auf die letzte Teilaufgabe wird stets von folgendem Empfangswert ausgegangen: | ||
| + | :$$\underline{y} = (0, 1, 0) =\underline{y}_2 | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| + | Die hier gewählte Indizierung aller möglichen Empfangsvektoren kann der Grafik entnommen werden. Der meist betrachtete Vektor $\underline{y}_2$ ist hierbei rot hervorgehoben. Für die Teilaufgabe (6) gilt dann: | ||
| + | :$$\underline{y} = (1, 1, 0) =\underline{y}_6 | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| + | Zur Decodierung sollen in der Aufgabe untersucht werden: | ||
| + | * die [[Syndromdecodierung]], die bei den hier betrachteten Codes als <i>Hard Decision Maximum Likelihood Detection</i> (HD–ML) vornimmt. <i>Hinweis:</i> Softwerte liegen beim BSC nicht vor. | ||
| + | * die symbolweise [[Soft–in Soft–out Decodierung]] (SISO) entsprechend dieses Abschnitts. | ||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[...]]. | ||
| + | * Das vom Decoder ausgewählte Codewort wird in den Fragen mit $\underline{z}$ bezeichnet. | ||
Revision as of 21:22, 6 December 2017
Wir betrachten in dieser Aufgabe zwei Codes:
- den Single Parity–Code ⇒ SPC (3, 2, 2):
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (0, 1, 1), \hspace{0.1cm} (1, 0, 1), \hspace{0.1cm} (1, 1, 0) \hspace{0.05cm} \big ) \hspace{0.05cm}, $$
- den Wiederholungscode ⇒ RC (3, 1, 3:
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (1, 1, 1) \hspace{0.05cm} \big ) \hspace{0.05cm}.$$
Der Kanal wird auf Bitebene durch das BSC–Modell beschrieben. Entsprechend der Grafik gilt dabei:
- $${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$
- $${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$
Hierbei bezeichnet $\epsilon$ die Verfälschungswahrscheinlichkeit.
Bis auf die letzte Teilaufgabe wird stets von folgendem Empfangswert ausgegangen:
- $$\underline{y} = (0, 1, 0) =\underline{y}_2 \hspace{0.05cm}. $$
Die hier gewählte Indizierung aller möglichen Empfangsvektoren kann der Grafik entnommen werden. Der meist betrachtete Vektor $\underline{y}_2$ ist hierbei rot hervorgehoben. Für die Teilaufgabe (6) gilt dann:
- $$\underline{y} = (1, 1, 0) =\underline{y}_6 \hspace{0.05cm}. $$
Zur Decodierung sollen in der Aufgabe untersucht werden:
- die Syndromdecodierung, die bei den hier betrachteten Codes als Hard Decision Maximum Likelihood Detection (HD–ML) vornimmt. Hinweis: Softwerte liegen beim BSC nicht vor.
- die symbolweise Soft–in Soft–out Decodierung (SISO) entsprechend dieses Abschnitts.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel ....
- Das vom Decoder ausgewählte Codewort wird in den Fragen mit $\underline{z}$ bezeichnet.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)